Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 11.Problemas - Ex. 73

Duas estrelas idênticas, cada uma com massa M, giram em torno do centro de massa das duas estrelas. Cada órbita é circular e possui raio R, de modo que as duas estrelas estão sempre em lados opostos do circulo. a) Ache a força gravitacional de uma estrela sobre a outra. b) Ache a velocidade orbital de cada estrela e o período da órbita. c) Qual deve ser a energia necessária para separar as duas estrelas até uma distancia infinita?

Passo 1

Opa, bora resolver esse problema!

Aqui a gente tem duas estrelas de mesma massa m e elas estão orbitando em torno uma da outra!

Sabemos que o raio da órbita é R e elas estão sempre do lado oposto. Ou seja a distância entre elas é 2 R .

Aqui vamos utilizar a equação F g = G m T m / r 2 para calcular F g . E aplicar a 2ª lei de Newton ao movimento circular de cada estrela para encontrar a velocidade orbital e período.

Aplicaremos a expressão de conservação de energia para calcular a entrada de energia (trabalho) necessário para separar as duas estrelas até o infinito.

Veja só!

Passo 2

  1. O C , M está a meio caminho entre as duas estrelas, uma vez que possuem massas iguais. Seja R o raio da órbita para cada estrela, conforme esboçado na Figura a seguir:

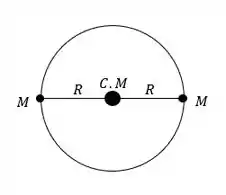
    2. As duas estrelas são separadas por uma distância 2 R ,

    então

    F g = G M 2 2 R 2

    F g = G M 2 4 R 2

    Tranquilo até aqui? 

    Passo 3

  2. E para encontrar a velocidade orbital de cada estrela e o período da órbita, fazemos:

    3. F g = m a r a d

    G M 2 4 R 2 = M v 2 R

    Então

    v = G M 2 R

    E

    T = 2 π R v = 2 π R 4 R G M

    T = 4 π R 3 G M

    Show!

    Passo 4

  3. Aplicando K 1 + U 1 + W o u t r o = K 2 + U 2 ao sistema das duas estrelas.

Separar até o infinito implica K 2 = 0   e U 2 = 0 .

K 1 = 1 2 M v 2 + 1 2 M v 2 = 2 1 2 M G M 4 R = G M 2 4 R

U 1 = - G M 2 2 R

Assim, a energia necessária é

W o u t r a = - K 1 + U 1 = - G M 2 4 R - G M 2 2 R

W o u t r a = G M 2 4 R

Quanto mais próximas as estrelas e maior sua massa, maior sua velocidade orbital, menor sua

período orbital e maior a energia necessária para separá-los.

E aí! sacou? Responde Aí!

Resposta

  1. G M 2 / 4 R 2
  2. v = G M 2 R e T = 4 π R 3 G M
  3. G M 2 4 R
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A sua espaçonave, o Andarilho Errante, pousa no mistérioso planeta Mongo. Como engenheiro e cientista-chefe, você efetuaas seguintes medidas: uma pedra de massa igual a 2,50k g jogada para cima a part
A garra de um martelo é usada para arrancar um prego de uma tábua (Figura 11.38 ). O martelo faz um ângulo de 60 ° com a tábua, e a força F 1 → necessária para arrancar o prego possui módulo igual a 5
12.59. a) Suponha que você esteja no equador da Terra e observe um satélite passando bem em cima de sua cabeça e movendo-se de oeste para leste no céu. Exatamente 12,0 horas depois você vê esse satéli
Uma ponte levadiça homogênea deve ser mantida suspensa a um ângulo de 30 ° acima da horizontal, para permitir que os navios passem por baixo dela. A ponte pesa 45000 N e tem 1,40 m de comprimento. Um
a) A Figura 11.46 mostra uma viga uniforme com 6,0 m de comprimento sendo suspensa em ponto situado a 1,0 m à direita do seu centro. A viga pesa 140 N e faz um ângulo de 30,0 ° com a vertical. Na extr