Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 10.Problemas - Ex. 80

Em uma catapulta de mola, a constante da mola é igual a 400 N/m e a mola sofre uma compressão de 0,15 m. Quando ela é disparada, 80% da energia potencial elástica armazenada na mola é convertida em energia cinética para uma bola uniforme de 0,0590 kg que estava rolando sem deslizar na base de uma rampa. A bola continua a rolar sem deslizar subindo a rampa com 90% da energia cinética que ela possuía na base convertida em energia potencial gravitacional no momento em que ela pára.

a) Determine a velocidade do centro de massa da bola na base da rampa.

b) Nessa posição, qual é a velocidade de um ponto no topo da bola?

c) Nessa posição, qual é a velocidade de um ponto na base da bola?

d) Qual é a altura vertical máxima acima da base da rampa atingida pela bola?

Passo 1

Aplicaremos a conservação de energia. Tendo uma informação importante que é: a bola termina com ambos energia cinética translacional e rotacional.

Para determinar a velocidade do centro de massa, precisamos da relação que envolve a porcentagem (dada no problema)

K 1 = 0,8   U e l

Vamos calcular a energia potencial elástica

U e l = 1 2 k x 2

U e l = 1 2 ( 400 N / m ) ( 0,15   m ) 2

U e l = 4,5   J

Então,

K 1 = 0,8   ( 4,5 )

K 1 = 3,6   J

Dá pra encontrar a velocidade por meio de K 1 , então

K 1 = 1 2 m v c m 2 + 1 2 I c m ω 2

Sendo ω = v c m R ,

K 1 = 1 2 m v c m 2 + 1 2 I c m ( v c m R ) 2

O momento de inércia é I c m = 2 5 m R 2

K 1 = 1 2 m v c m 2 + 1 2 ( 2 5 m R 2 ) ( v c m R ) 2

K 1 = 1 2 m v c m 2 + 1 5 m v c m 2

K 1 = 7 10 m v c m 2

3,6   J = 7 10 m v c m 2

Então...

v c m = 36 7 m

v c m = 36 7 ( 0,059   k g )

v c m = 9,34   m / s

Passo 2

A seguinte figura representa o movimento de translação e rotação. Vamos usá-la para resolver as letras (b) e (c).

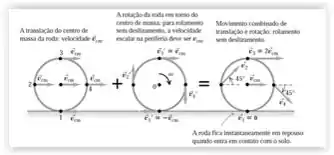
Para a velocidade de um ponto no topo da bola, vamos observar a figura

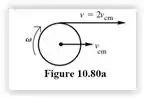
A velocidade é duas vezes v c m , então

v = 2 v c m

v = 2 ( 9,34   m / s )

v = 18,68   m / s

Quando a velocidade de um ponto for na base da bola, então v = 0 .

Passo 3

Resolvendo a letra (d), o enunciado nos diz que “A bola continua a rolar sem deslizar subindo a rampa com 90% da energia cinética que ela possuía na base convertida em energia potencial gravitacional no momento em que ela pára.” Assim,

U 2 = 0,9   K 1

Então,

U 2 = 0,9   3,6   J = 3,24   J

Sabemos que U 2 = m g h , logo

3,24   J = ( 0,059   k g ) ( 9,8   m / s 2 ) h

h = 5,6   m

Resposta

a) v c m = 9,34   m / s

b) v = 18,68   m / s

c)   v = 0

d) h = 5,6   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um cano de paredes finas rola no chão. Qual é a razão entre a energia cinética de translação do cano e a energia cinética de rotação em relação ao eixo central paralelo à sua maior dimensão?
Uma roda homogênea de massa 10,0k g e raio 0,400m está montada rigidamente em um eixo que passa pelo centro (Fig. 11-62). O raio do eixo é 0,200m e o momento de inércia do conjunto roda-eixo em relaçã
Um automóvel que se move a 80 k m / h possui pneus com 75 c m de diâmetro. ( a ) Qual é a velocidade angular dos pneus em relação aos respectivos eixos? ( b ) Se o carro é freado com aceleração consta
Um carro se move a 80 k m / h em uma estrada plana no sentido positivo de um eixo x . Os pneus tês um diâmetro de 66 c m . Em relação a uma mulher viajando no carro e em termos dos vetores unitários,
Um aro de 140 k g rola em um piso horizontal de tal forma que o centro de massa tem uma velocidade de 0,15 m / s . Qual é o trabalho necessário para fazê-lo parar?