Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 10.Problemas - Ex. 81

Quando uma roda rola ao longo de uma superfície horizontal com velocidade constante, as coordenadas de um ponto na periferia da roda são x t = R [ 2 π t T - sin ⁡ 2 π t T ] e y t = R [ 1 - cos ⁡ ( 2 π t T ) ] , onde R e T são constantes.

a) Faça um desenho da trajetória do ponto de t = 0 a t = 2 T . Uma curva com essa forma é denominada ciclóide.

b) Qual é o significado das constantes R e T?

c) Ache os componentes x e y do vetor velocidade e da aceleração do ponto em qualquer instante.

d) Ache os instantes em que o ponto fica instantaneamente em repouso. Quais são os componentes x e y da aceleração nesses instantes?

e) Ache o módulo da aceleração do ponto. Ele depende do tempo? Compare com o módulo da aceleração de uma partícula em movimento circular uniforme, a r a d = 4 π R 2 T 2 . Explique seu resultado para o módulo da aceleração do ponto na roda que gira, usando o conceito de que a rolagem é um movimento combinado de rotação e translação.

Passo 1

O desenho da trajetória seria:

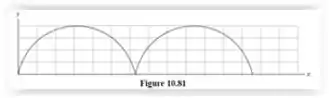
As constantes R e T representam o raio da roda (y que varia de 0 a 2R) e T é o período de rotação da roda, respectivamente.

Passo 2

Para acharmos os componentes x e y do vetor velocidade e da aceleração do ponto em qualquer instante, lembramos do diferencial

v x = d x d t = d d t R [ 2 π t T - sin ⁡ 2 π t T ]

v y = d y d t = d d t { R [ 1 - cos ⁡ ( 2 π t T ) ] }

Resolvendo as derivadas,

v x = d d t R × [ 2 π t T sin ⁡ 2 π t T ] + { R × d d t [ 2 π t T - sin ⁡ 2 π t T ] }

= 0 + R 2 π T - R × 2 π cos ⁡ ( 2 π t ) T

= 2 π R T - [ R 2 π cos ⁡ ( 2 π t ) T ]

v x = 2 π R T [ 1 - cos ⁡ ( 2 π t T ) ]

Para y:

v y = d d t R × [ 1 - cos ⁡ ( 2 π t T ) ] + R d d t [ 1 - cos ⁡ ( 2 π t T ) ]

v y = 0 + R d d t [ 1 - cos ⁡ ( 2 π t T ) ]

v y = 2 π t T sin ⁡ 2 π t T

Para a aceleração:

a x = d 2 x d t 2

= d d t { 2 π R T [ 1 - cos ⁡ ( 2 π t T ) ] }

a x = ( 2 π T ) 2

Em y:

a y = d 2 y d t 2

= d d t { 2 π t T sin ⁡ 2 π t T }

a y = ( 2 π T ) 2 R cos ⁡ ( 2 π t T )

Passo 3

Os instantes em que o ponto fica instantaneamente em repouso, vamos descobrir as componentes x e y da aceleração nesses instantes.

Fazendo v x = v y = 0 , então v x = 2 π t T = 2 π ou qualquer múltiplo de 2π. Os tempos são múltiplos inteiros do período T.

v x = 2 π R T [ 1 - cos ⁡ ( 2 π ) ]

v x = 2 π R T [ 1 - 1 ]

v x = 0

Para a aceleração, nesse tempo, a x = 0 . Já em y,

a y = ( 2 π T ) 2 R cos ⁡ ( 2 π )

a y = ( 2 π T ) 2 R × 1

a y = 4 π 2 R T 2

Passo 4

O módulo da aceleração do ponto, será

a = a x 2 + a y 2

a = 0 + 4 π 2 R T 2

a = ( 2 π T ) 2 R

Esse resultado não depende do tempo. Consiste na magnitude da aceleração radial para um ponto que se move em um círculo de raio R com velocidade angular constante 2 π T .

Resposta

a) Figura.

b) As constantes R e T representam o raio da roda (y que varia de 0 a 2R) e T é o período de rotação da roda, respectivamente.

c) v x = 2 π R T [ 1 - cos ⁡ ( 2 π t T ) ] e v y = 2 π t T sin ⁡ 2 π t T ; a x = ( 2 π T ) 2 e a y = 4 π 2 R T 2 .

d)   v x = 2 π t T = 2 π ; a x = 0 e a y = 4 π 2 R T 2

e) a = ( 2 π T ) 2 R

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um carro de 1000 k g tem quatro rodas de 10 k g . Quando o carro está em movimento, que fração da energia cinética total se deve à rotação das rodas em torno dos respectivos eixos? Suponha que as roda
Uma esfera maciça e homogênea rola para baixo em um plano inclinado. ( a ) Qual deve ser o ângulo de inclinação do plano para que a aceleração linear do centro da esfera tenha um módulo de 0,10 g ? (
Uma esfera oca, com 0,15 m de raio e momento de inércia I = 0,040 k g m ² ² em relação a uma reta que passa pelo centro de massa , rola sem deslizar, subindo uma superfície com uma inclinação de 30 °
A figura abaixo mostra a velocidade escalar v em função do tempo t para um objeto de 0,5 k g e 6 c m de raio que rola suavemente para baixo em uma rampa de 30 ° . A escala do eixo das velocidades é de
Na figura abaixo uma bola maciça rola suavemente a partir do repouso (começando na altura H = 6 m ) até deixar a parte horizontal no fim da pista, a uma altura h = 2 m . A que distância horizontal do