Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 4.Exercícios e Problemas - Ex. 49
Você se encontra a da parede de uma casa e deseja arremessar uma bola para seu colega que está a da parede oposta. Tanto o arremesso acima do solo quanto a interceptação da bola ocorrem acima do solo.
a. Qual é o mínimo valor de velocidade que fará com que a bola ultrapasse o telhado?
b. Em que ângulo a bola deve ser arremessada?
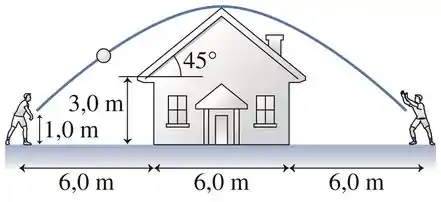
Passo 1
Esquematizando o desenho
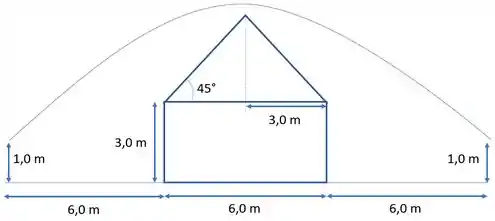
Geometricamente, o telhado é um triângulo isósceles, ou seja, galerinha, a=b, assim a base total que é 6m pode ser dividida por 2 que vai dar 3 m. Só que se você perceber que já temos um ângulo de 45° que foi indicado pelo exercício e que a altura é 90°, o ângulo que falta é 45°, portanto é um outro triângulo isósceles, assim a altura vai ser 3 m também.
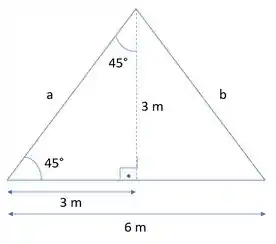
Sabendo da altura do telhando, a altura total da casa é de , mas considerando que a bola é lançada a um metro a distância do movimento em relação a y é de , assim vamos as equações.
Passo 2
- O exercício quer saber a velocidade inicial da bola, para isso, vamos considerar que a velocidade final é zero quando o garoto pega a bola do outro lado da casa, assim encontramos a velocidade inicial de y
Já sabemos a velocidade inicial de y e agora? Para descobrir a velocidade inicial de x é necessário lembrar em x, o movimento é uniforme, e em y é variado, então quem determina o tempo é o movimento vertical, ouuuu seja, temos que encontrar o tempo em relação y
E assume os valores e s e como zero não é uma solução interessante, vamos usar . Encontramos o tempo, a gora vamos descobrir a velocidade inicial de x
E, finalmente, o modulo da velocidade é
Ufa! Acabamos (a), agora falta o (b)!
Passo 3
b. Para saber a direção do vetor, usaremos a tangente das velocidades inicias de y e x, assim