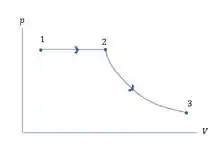
Um certo gás ideal possui calor especifico molar a volume constante . Uma amostra desse gás inicialmente ocupa um volume a uma pressão e uma temperatura absoluta . O gás se expande isobaricamente até um volume , a seguir sofre uma expansão adiabática até um volume final igual a . a) Desenhe um diagrama dessa sequencia de processo. b) Calcule o valor absoluto de calor trocado com as vizinhanças nessa sequencia de processos e determine o sentido do fluxo do calor.
Passo 1
Para pressão constante, . Para um processo adiabático de um gás ideal,
e
Passo 2
- O diagrama é esboçado na figura a seguir:
- O trabalho realizado é:
- A maneira mais direta de encontrar a temperatura é encontrar a razão entre a pressão e o volume final e o original e tratar o ar como um gás ideal.
- Desde que
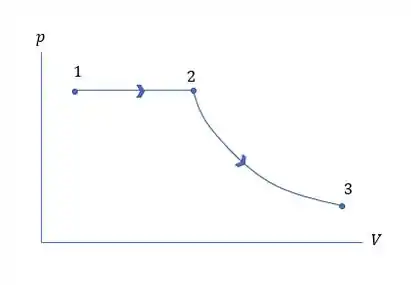
Passo 3
E então
Observe que é a pressão absoluta.
Passo 4
desde que Então,
Passo 5
Essa quantidade de calor flui para o gás, desde .