Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 28.Problemas Adicionais - Ex. 79
Em um certo instante, é a velocidade de um próton em um campo magnético uniforme . Para esse instante, determine (a) a força magnética que o campo exerce sobre próton, em termo dos vetores unitários; (b) o ângulo entre e ; (c) o ângulo entre e .
Passo 1
A gente tira lá da teoria a seguinte expressão para a contribuição do campo magnético para a força é:
Nos foi dado a velocidade do próton e o campo magnético ao qual ele está submetido. Vamos, então, subsitutir esses valores na equação.
Passo 2
Vamos ao calculo da força, teremos um produto vetorial de e e nesse caso o melhor jeito de sair é com matriz, sugiro aqui multiplicarmos pela carga depois de encontrar o valor do produto pra não fazer salada!
Lembrando que você deve respeitar as ordens ou vai dar xabu aqui no sinal, daí tu pode fazer o determinante pela regra de cramer ou Laplace, mas pra gente ganhar um tempo vou trazer o resultado final aqui:
Obs: O valor foi colocado ali pela unidade do campo em .
Passando a carga para o outro lado e convertendo em coulombs temos:
Passo 3
Vamos responder tanto o item b. sem fazer nenhuma conta, só com teoria, quer ver? Lembra da regra da mão direita?
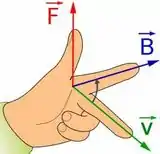
Ela só mostra como funciona na verdade o sistema de três eixos entre campo magnético força e velocidade.
Por definição quando calculamos o produto vetorial entre e encontramos uma força fora do plano, que é perpendicular aos dois vetores.
Sendo assim o ângulo entre e é e isso responde a letra b.
Passo 4
E pra responder a letra c., vamos lembrar da definição de produto escalar entre dois vetores:
Onde é o ângulo entre os vetores e . Beleza? Sendo assim, podemos isolar esse ângulo:
Fazendo o produto escalar:
Fazendo o módulos de cada um deles:
E:
Dessa forma:
E isso dá:
Beleza?? Acabou!
Resposta
- ;