Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 28.6 - Ex. 32
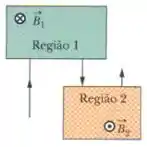
Na Fig. 28-42, um elétron com uma energia cinética inicial de penetra na região 1 no instante . Nessa região existe um campo magnético uniforme dirigido para dentro do papel, de módulo . O elétron descreve uma semicircunferência e deixa a região 1, dirigindo-se para a região 2, situada a de distância da região 1. Existe uma diferença de potencial entre as duas regiões, com uma polaridade tal que a velocidade do elétron aumenta no percurso entre a região 1 e a região 2. Na região ,2 existe um campo magnético uniforme dirigido para fora do papel, de módulo . O elétron descreve uma semicircunferência e deixa a região 2. Determine o instante t em que isso acontece.
Passo 1
E aí! tudo certinho? 😊
Aqui um elétron entra na região 1 que existe um campo magnético aplicado, depois percorre uma distância até uma região 2 que existe uma diferença de potencial (logo ele acelera) e entra em outra região que tem um campo oposto da primeira região, e é pedido o instante que o elétron deixa a segunda região.
Tem ideia de como fazemos isso? 🤔
Passo 2
Como, de acordo com a Eq. 28-17,
o tempo total é
O tempo que o elétron passa no espaço entre as regiões onde existe campo magnético (sendo
acelerado de acordo com a Eq. 2-15) deve ser calculado separadamente.
Calculando a energia cinética
onde e é a massa do elétron , , , e
Tranquilo até aqui? 😉
Passo 3
Na Eq. 2-15, na qual é a energia cinética inicial do elétron e d é a distância
usando , , e
usando baskara conseguimos .
Agora substituindo os outros valores em (, e )
O que achou? Responde Aí! 😉
