Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 12.Exercícios e Problemas - Ex. 53

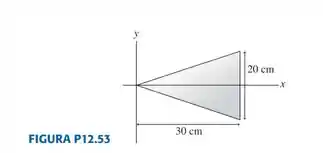
Uma chapa de aço de 800   g tem a forma do triângulo isósceles mostrado na FIGURA P12.53. Quais são as coordenadas x e y do centro de massa?

Sugestão: divida o triângulo em tiras verticais de largura d x cada uma, depois relacione a massa d m de uma tira dessas na posição x com os valores de x   e de d x .

Passo 1

Bem, vamos dividir esse triângulo em pequenas faixas retangulares como a nossa sugestão nos informou:

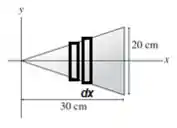
Repare que a areazinha d A de um retângulo desses pode ser obtida fazendo...

C ⋅ d x = d A

Onde C é o comprimento desse retângulo. Podemos dizer que esse retângulo está a uma distância x da origem:

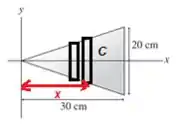
Por semelhança de triângulos entre o grandão e esse com a base C e altura x :

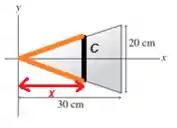
Concluímos que C vale...

20 C = 30 x   →

C = 2 3 x

Então...

C ⋅ d x = d A   →

2 3 x d x = d A

Passo 2

Por outro lado, sabemos que a massa total M está para a área total A , assim como d m está para d A , já que a superfície é uniforme:

M A = d m d A     →

d A = A M d m

Então...

2 3 x d x = A M d m     →

d m = 2 M 3 A x d x

De acordo com a teoria, a o x do centro de massa pode ser então calculado pela fórmula:

x c m = 1 M ∫     x   d m       →

Então... (Se lembrando de que x está variando de 0 a 30 c m )...

x c m = 1 M ∫ 0 30 x   2 M 3 A x d x       →

x c m = 2 3 A ∫ 0 30 x 2 d x       →

x c m = 2 3 A x 3 3 0 30       →

x c m = 2 3 A 30 3 3       →

A área é a área de a chapa triangular (Base vezes altura sobre 2):

A = 30 ⋅ 20 2 = 30 ⋅ 10

Então...

x c m = 2 3 30 ⋅ 10 30 3 3       →

x c m = 20

Passo 3

Como a superfície esta perfeitamente simétrica em relação a y , não precisamos. Calcular nada para ele, afinal...

y c m = 0

Resposta

Centro de massa:

20 ,   0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A molécula de metano ( C H 4 ) possui quatro átomos de hidrogênio localizados nos vértices de um tetraedro regular de 0,18 n m de lado, com o átomo de carbono no centro do tetraedro (figura 9-48). Det
Um corpo maciço de massa m , colocado sobre uma superfície horizontal sem atrito, está preso a um fio que é enrolado em torno de um pilar cilíndrico vertical preso à superfície. Assim, quando o corpo
O momento de inércia da Terra em relação ao seu eixo vale, aproximadamente, 8,03 × 10 37 k g ⋅ m 2 . (a) Como a Terra é quase esférica, suponha que seu momento de inércia possa ser escrito como I = C
56. Determine o momento de inércia em torno do eixo do objeto mostrado na FIGURA P12.56.
52. Um triângulo equilátero com 5,0c m de lado gira em torno de seu centro de massa a 120r p m . Quanto vale a velocidade de um vértice do triângulo?