Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 9.3 - Ex. 20
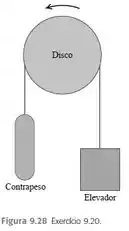
Em um charmoso hotel do século , um elevador antigo está conectado a um contrapeso por um cabo que passa por um disco giratório de de diâmetro (Figura ). O elevador sobe e desce ao se girar o disco, e o cabo não desliza pela borda do disco, mas gira com ele.
a) A quantas deve o disco girar para que o elevador suba a ?
b) Para colocar o elevador em movimento, ele deve ser acelerado a . Qual deve ser a aceleração angular do disco, em ?
c) A qual ângulo (em radianos e em graus) o disco girou, após levantar o elevador entre dois andares?
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente encontrar (a) a velocidade angular em do disco, para que o elevador suba a , (b) a aceleração angular do disco, em , e (c) o ângulo (em radianos e em graus) que o disco girou, após levantar o elevador .
O problema nos dá o raio do disco:
E a velocidade linear do elevador:
Então, vamos precisar encontrar a velocidade angular por meio da equação:
E depois converter o resultado para . Em seguida, vamos determinar a aceleração angular:
E o ângulo através da equação:
Vamos lá!
Passo 2
Vamos começar calculando a velocidade angular:
Substituindo os dados que vimos no passo , temos:
Mas sabemos que , então temos que a velocidade angular em é:
Passo 3
Sabendo que a aceleração e que a aceleração angular, vamos ter:
E substituindo os valores, obtemos:
Passo 4
Agora para determinar o ângulo percorrido pelo arco de comprimento , podemos usar a fórmula do comprimento de arco:
Então, isolando na equação e substituindo os valores, temos:
E em graus temos:
Valeu, galera! Até a próxima! 😉