Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 24.Problemas - Ex. 57

Para o circuito de capacitores indicado na figura abaixo, a diferença de potencial através de a e b é de 12   V . Ache (a) a energia total armazenada nesse circuito e (b) a energia armazenada no capacitor de 4,8   μ F .

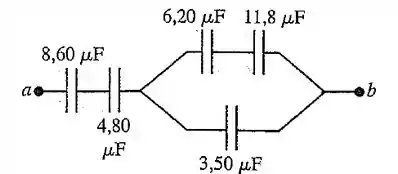
Passo 1

Temos para associação de capacitores:

i ) C a p a c i t o r e s   e m   p a r a l e l o :

C e q = C 1 + C 2 + . . .

Q = Q 1 + Q 2 + . . .

V 1 = V 2 = V

i i ) C a p a c i t o r e s   e m   s é r i e :

1 C e q = 1 C 1 + 1 C 2 + . . .

Q 1 = Q 2 = Q

V = V 1 + V 2 + . . .

Passo 2

letra a)

Como queremos a energia total e sabemos a diferença de potencial total, podemos escrever:

U t o t a l = 1 2   C e q V a b 2

Precisamos então calcular a diferença de potencial.

Passo 3

Os capacitores C 1 = 6,2   μ F e C 2 = 11,8   μ F estão em série, logo:

1 C 12 = 1 C 1 + 1 C 2

1 C 12 = 1 6,2 ⋅ 10 - 6 + 1 11,8 ⋅ 10 - 6

1 C 12 = ( 11,8 + 6,2 ) 73,16 ⋅ 10 - 6

1 C 12 = 18 73,16 ⋅ 10 - 6

C 12 = 4,1 ⋅ 10 - 6   F

Passo 4

Os capacitores C 12 e C 3 estão em paralelo, logo:

C 123 = C 12 + C 3

C 123 = 4,1 ⋅ 10 - 6   + 3,5 ⋅ 10 - 6  

C 123 = 7,6 ⋅ 10 - 6   F

Passo 5

Os capacitores C 123 , C 4 e C 5 estão em série, logo:

1 C e q = 1 C 123 + 1 C 4 + 1 C 5

1 C e q = 1 7 , 6 ⋅ 10 - 6 + 1 8,6 ⋅ 10 - 6 + 1 4,8 ⋅ 10 - 6

1 C e q = 41,58 + 36.48 + 65,36 313,728 ⋅ 10 - 6

C e q = 2,19 ⋅ 10 - 6   F

Passo 6

Agora que sabemos a capacitância equivalente, podemos calcular a energia total.

U t o t a l = 1 2   C e q V a b 2

U t o t a l = 1 2 2,19 ⋅ 10 - 6 ⋅ 12 2

U t o t a l = 1,58 ⋅ 10 - 4   J

Passo 7

letra b)

Precisamos encontrar agora a energia armazenada no capacitor C 5 = 4,8 μ F .

Para isso podemos, podemos encontrar a sua carga e depois usar a relação:

U 5 = Q 5 2 2 C 5

Passo 8

Para capacitores em série vale a relação:

Q 4 = Q 5 = Q 123 = Q

Podemos agora achar Q 5 :

Q 5 = C e q V a b

Q 5 = 2,19 ⋅ 10 - 6 ⋅ 12

Q 5 = 2,63 ⋅ 10 - 5     C

Passo 9

A energia então será:

U 5 = 2,63 ⋅ 10 - 5   2 2 4,8 ⋅ 10 - 6

U 5 = 7,21 ⋅ 10 - 5     J

Resposta

letra a) U t o t a l = 1,58 ⋅ 10 - 4   J

letra b) U 5 = 7,21 ⋅ 10 - 5     J

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma carga q é colocada lentamente na superfície de uma bolha de sabão, de raio R a . Devido à repulsão mútua existente entre as cargas superficiais, o raio aumenta ligeiramente para R . Por causa da e
Uma lâmina dielétrica de espessura h é introduzida entre as placas de um capacitor de placas paralelas de separação d . Mostre que a capacitância é dada por C = k ϵ 0 A k d - b k - 1 (Sugestão: Deduza
O espaço entre duas cascas esféricas condutoras concêntricas de raios b e a (onde ba ) é preenchido com uma substância de constante dielétrica k . Existe uma diferença de potencial V entre as cascas i
Um condutor esférico de raio R tem uma carga Q sobre sua superfície. Qual é o campo elétrico (a) interior e (b) exterior ao condutor? (c) Que quantidade de energia eletrostática está armazenada numa c
Um relógio de parede circular tem uma face com um raio de 15c m . Seis voltas de fio estāo enroladas em torno do seu perimetro; o fio conduz uma corrente de 2,0 A no sentido horário. O relógio é posic