Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 28.1 - Ex. 59

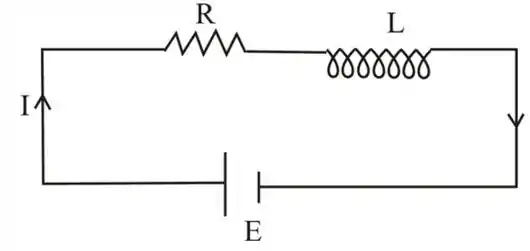
Um circuito de uma boba com resistência igual a 8,00   Ω e auto - indutância igual a 4,00   m H , uma chave aberta e uma bateria ideal de 100V – todos conectados em série. Em t = 0 a chave é fechada. Determine a corrente e sua taxa de variação nos instantes a   t = 0 ,   b   t = 0,100   m s ,   c t = 0,500   m s   e   d t = 1,00   m s .

Passo 1

Falaaaaaa pessoal, show de bola??

Bora resolver esse exercício na maciotaaaaa, então siimboraa!!

Dados

Resistencia da bobina R = 8 Ω

Indutância L = 4 × 10 - 3 H

E = 100 V

Passo 2

Temos a equação que descreve a corrente no circuito como

E = R I + L d I d t

Em t = 0 ,   I = 0 (que aumenta assim que a chave está no modo ON).

Valor final

I 0 = E / R

A qualquer momento ‘t’, a expressão atual é obtida como

I = I 0 ( 1 - e x p ⁡ ( - t / τ ) )  

Onde τ = L / R , é a constante de tempo do circuito.

Passo 3

  1. Então, em t = 0 ,   I = 0

    2. d I d t = E L = 100 4 × 10 - 3  

    = 25   k A / s

    Passo 4

  2. E m   t = 0,1   m s  

    3. I = 100 8 1 - exp ⁡ - 0.1 × 10 - 3 × 8 4 × 10 - 3

    I = 2.27   A

    A taxa de variação da corrente é obtida em t = 0,1 m s

    Como

    d I d t = 1 L E - R I = 100 - 8 × 2.27 4 × 10 - 3

    = 20.46   k A / s

    Passo 5

  3. Em t = 0.5   m s

    4. = 100 8 1 - exp ⁡ - 0.5 × 10 - 3 × 8 4 × 10 - 3 = 7.90   A

    d I d t = 1 4 × 10 - 3 100 - 7.9 × 8 = 9.20   k A / s

    Passo 6

  4. Em t = 1   m s

I = 100 8 1 - exp ⁡ - 1 × 10 - 3 × 8 4 × 10 - 3 = 10.81   A

d I d t = 1 4 × 10 - 3 100 - 10.81 × 8 = 3.38     k A / s

Resposta

  1. I = 0 A e 25.0kA/s
  2. 2.27A e 20.5kA/s
  3. 7.90A e 9.20kA/s
  4. 10.8A e 3.38kA/s
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um circuito consiste em uma bobina de 4,00 mH,umresistor de 1502,uma bateria ideal de 12,0 Ve uma chave aberta－todos conectados em serie.Depois que a chave fechada:(a)Quale a taxa inicial de aumento d
Dado o circuito mostrado na Figura 28-56,o indutor temresistencia interna desprezivele a chave S esteve aberta por um longotempo.A chavee,entao,fechada.(n)Determine a corrente na bateria,a corrente no
Um circuito consiste em uma bobina que tem auto-indutância igual a 5,00 mH e a resistência interna igual a 15,0Ω , uma bateria ideal de 12,0 V e uma chave aberta – todos conectados em série (Figura 28
No circuito mostrado na Figura 28-54, seja ε 0 = 12,0V , R = 3,00Ω e L = 0,600H . A chave é fechada no instante t = 0 . Durante o tempo desde t = 0 até t = L / R , determine:a) A quantidade de energia
Tome como referência o Exercício 30.23. (a) Qual é a taxa com que a bateria está fornecendo energia elétrica ao circuito logo após ele estar fechado? (b) Quando a corrente tiver alcançado seu valor co