Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Moysés - Vol. 3- Ed: 1º - Capítulo 10.Problemas - Ex. 9

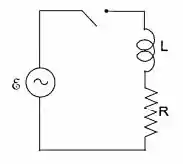
No circuito da figura, fecha-se a chave em t = 0 , com ε = ε 0 sin ⁡ ω t + π 4 . (a) Ache a corrente I t , incluindo o termo transiente e a solução estacionaria. (b) Para que valor de ω o transiente desaparece?

Passo 1

Nesse problema iremos utilizar as relaçoes chegadas no capítulo, onde já nos é dado os exemplos de como obter para esse caso em especifico. Primeiro vamos calcular a impedância do circuito e após isso, poderemos aplicar já para:

I t = ε 0 Z ⋅ e i ω t + π 4 - φ L + e i π 4 - φ L

Onde o segundo termo dentro do colchetes é a nossa solução estacionaria e φ L a defasagem, dada no capítulo.

Passo 2

Bom, como dito no passo 1, vamos começar achando a impedância para o circuito em série. Temos que ela é dada por:

Z = R + i ω L

Mas precisamos do módulo da nossa impedância. Podemos então fazer:

Z = R 2 + ω L 2 .

Aplicando agora na nossa relação dada no passo 1, vamos ter que:

I t = ε 0 Z ⋅ e i ω t + π 4 - φ L + e i π 4 - φ L = ε 0 R 2 + ω L 2 ⋅ e i ω t + π 4 - φ L + e i π 4 - φ L

Pegando a parte real apenas da nossa solução, vamos ter que:

I t = ε 0 R 2 + ω L 2 ⋅ sin ⁡ ω t + π 4 - φ L + sin ⁡ π 4 - φ L

Sendo essa nossa solução com o termo estacionário. O termo φ L é determinado pelo arctan ⁡ ω L R , que foi obtido no exemplo do capitulo na seção 10.7 .

Passo 3

Queremos agora sumir com todos os termos transientes da solução. Ou seja, queremos que nossa solução não dependa de L . Para isso, precisamos que nossa frequência ω seja

ω = R L .

Assim, nossa solução toda não dependerá de L .

Resposta

  1. I t = ε 0 R 2 + ω L 2 ⋅ sin ⁡ ω t + π 4 - φ L + sin ⁡ π 4 - φ L
  2. ω = R L
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A tensao do gerador na Figura 29-40edada por S = ( 100 V) c o s ⁡ ( 2 π f t ) . a)Para cada ramo,qual e a corrente de pico e qual e a fase da corrente relativa a fase da tensao do gerador?(b)Na freque
APLICACAO EM ENGENHARIA Um metodo para determinar a compressibilidade de um material dieletrico usa um circuito LC com um capacitor de placas paralelas.O dieletricoinserido entre as placas e a variaca
Um circuito consiste em um gerador ac ideal,um capacitor e um indutor ideal,todos conectados em serie.A carga no capacitor edada por Q = 15 μ C cos ⁡ ω t + π 4 , onde ω = 1250 r a d s a)Determine a co
APUCACAO EM ENGENHARIA Ocircuito mostrado na Figura 29-37 e um filtro de corte.(Considere que a saida esteja conectada a uma carga que conduz uma corrente insignificante.)(a)Mostre que o filtro de cor
PLANILHA ELETRONICA Usando uma planilha eletrônica faca um grafico de V.versus a frequencia de entrada f e um grafico do angulo de fase 8 versus a frequencia de entrada para o filtro passa-baixas dos