Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 27.9 - Ex. 65

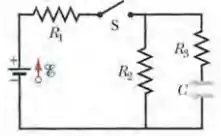
No circuito da Fig. 27-65, ε = 1,2 k V , C = 6,5 μ F e R 1 = R 2 = R 3 = 0,73 M % O M E G A . Com o capacitor C totalmente descarregado, a chave S é fechada bruscamente no instante t = 0 . Determine, para o instante t = 0 , (a) a corrente i 1 no resistor 1; (b) a corrente i 2 no resistor 2; (c) a corrente i 3 no resistor 3. Determine, para t % i n f i n i t y ( ou seja, após várias constantes de tempo), (d) i 1 , (e) i 2 , (f) i 3 . Determine a diferença de potencial V 2 no resistor 2 (g) em t = 0 e (h) para t → ∞ . (i) Faça um esboço do gráfico de V 2 em função de t no intervalo entre esses doi s instantes extremos.

Passo 1

Olá, meu amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.

Neste circuito temos um resistor R 1 antes da chave s , um resistore R 3 que está em série com um capacitor e estes dois estão em paralelo com um resistor, e basicamente queremos saber a situação do circuito em dois momentos um quando fechamos a chave S e outro, depois da chave ter ficado muito tempo fechada.

Passo 2

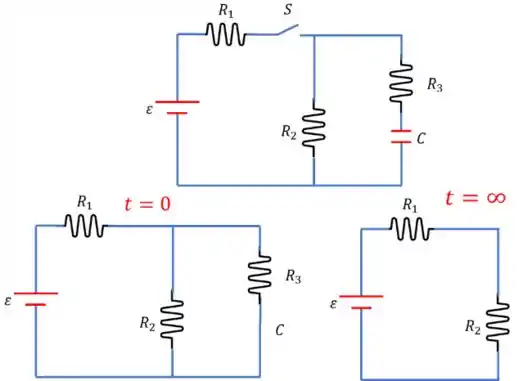
No instante t = 0, o capacitor está totalmente descarregado e se comporta como um curto-

circuito. Seja i 1 a corrente em R 1 , considerada positiva se o sentido for para a direita. Seja i 2 a corrente em R 2 , considerada positiva se o sentido for para baixo. Seja i 3 a corrente em R 3 , considerada positiva se o sentido for para baixo. De acordo com a regra dos nós,

i 1 = i 2 + i 3 .

Aplicando a regra das malhas à malha da esquerda, obtemos

ε – i 1 R 1 – i 2 R 2 = 0

e aplicando a regra das malhas à malha da direita, obtemos

i 2 R 2 – i 3 R 3 = 0

Como as resistências são todas iguais, podemos substituir R 1 , R 2 e R 3 por R, o que nos dá o seguinte sistema de equações:

i 1 = i 2 + i 3 .

ε – i 1 R – i 2 R = 0 ,

i 2 – i 3 = 0

Agora vamos resolver o sistema de equações!!

Passo 3

(a)Usando a última e a primeira equação temos:

i 2 = i 3

i 1 = 2 i 2

e usando a do meio

- i 1 R – i 1 2 R = - ε

3 2 R i 1 = ε

logo

i 1 = 2 3 ε R

onde

R = 0,73 ∙ 10 6 Ω

ε = 1,2 ∙ 10 3 V

i 1 = 2 1,2 ∙ 10 3 V 3 0,73 ∙ 10 6 Ω = 1,1 ∙ 10 - 3 A = 1,1 m A

Passo 4

(b) como

i 1 = 2 i 2

logo i 2 = 1,1 m A 2 = 0,55 m A

Passo 5

(c) Finalmente

i 3 = i 2

i 3 = 0,55 m A

Passo 6

(d)Para t → ∞ o capacitor está totalmente carregado e se comporta como um circuito aberto naquele ponto.

Assim, i 1 = i 2 , e a regra das malhas nos dá

ε – i R - i R = 0

i 1 = ε 2 R

i 1 = 1,2 ∙ 10 3 V 2 0,73 ∙ 10 6 Ω = 8,2 ∙ 10 - 4 A = 0,82 m A

(e)Como

i 2 = i 1

i 2 = 0,82 m A

(f) Como o capacitor age como um circuito aberto, não há fluxo de corrente nele, portanto, o resistor R 3 , então:

i 3 = 0

Passo 7

(g) A diferença de potencial através de R 2 é igual à corrente multiplicada pela resistência:

V 2 = I 2 R 2

Então em t = 0 , nós temos do item b) que i 2 = 0.55   m A :

V 2 = 5.5 ∙ 10 - 4 7.3 ∙ 10 5

= 401.5   V

Passo 8

(h) Em ( t   =   ∞ ) , temos, a partir da parte (e), ( I   =   0.882       m A ) , substitua para obter:

V 2 = 8.22 ∙ 10 - 4 7.3 ∙ 10 5

= 600.06   V

Passo 9

(i)

Em um instante genérico, as equações obtidas, aplicando ao circuito a regra dos nós e a regra

das malhas, são:

i 1 = i 2 + i 3

ε – i 1 R - i 2 R = 0

- q C – i 3 R + i 2 R = 0

Substituindo i 1 por i 2 + i 3 na segunda equação, obtemos ε – 2 i 2 R – i 3 R = 0 , o que nos dá i 2 = ε – i 3 R 2 R . Substituindo na terceira equação, obtemos

- q C – i 3 R + ε 2 – i 3 R 2 = 0

Substituindo i 3 por d q d t temos:

3 R 2 d q d t + q C = ε 2

Como a equação anterior é a equação de um circuito RC série com uma constante de tempo τ = 3 R C / 2 e uma fem aplicada ε / 2 , a solução é

q = C ε 2 1 - e 2 t / 3 R C .

A corrente no ramo do capacitor é

i 3 t = d q d t = ε 3 R e - 2 t / 3 R C

A corrente no ramo central é

i 2 t = ε 2 R – i 3 2 = ε 2 R - ε 6 R e - 2 t / 3 R C = ε 6 R 3 - e - 2 t / 3 R C

e a queda de tensão em R 2 é

V 2 t = i 2 R = ε 6 3 - e - 2 t / 3 R C

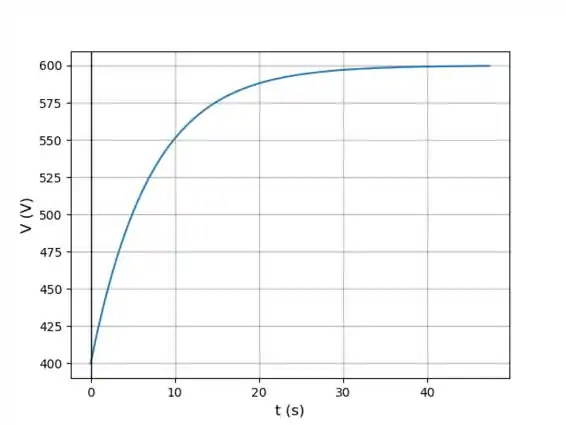
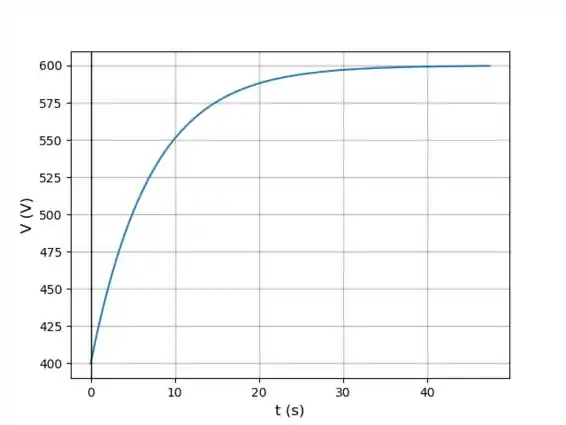
A figura a seguir mostra um gráfico de V 2 em função do tempo.

Resposta

(a) i 1 = 1,1 m A

(b) i 2 = 0,55 m A

(c) i 3 = 0,55 m A

(d) i 1 = 0,82 m A

(e) i 2 = 0,82 m A

(f) V 2 t = ε 6 3 - e - 2 t / 3 R C

(g) V 2 = 4,0 × 10 2 V

(h) V 2 = 6,0 × 10 2 V

(i)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma carga constante de 1,00m C está na placa carregada positivamente do capacitor de 5,00μ F mostrado na figura abaixo. Determine (a) a corrente na bateria e (b) as resistências R 1 ,R 2 , R 3 .
Em t = 0 o interruptor na Figura abaixo é girado para o contato b depois de ter estado no contato a por um longo tempo. (a) Determine a energia armazenada no capacitor depois de o interruptor ter sido
No circuito da Figura abaixo, C = 0 ,120μ F e ℇ = 100 Vℇ . A chave é girada para o contato b depois de ter estado no contato a por um longo tempo, e 4.00 s depois, a diferença de potencial no capacito
Para o circuito mostrado na Figura abaixo, C = 6,00μ F , ℇ = 100 Vℇ e R = 500 Ω . Depois de ter estado em contato com a por um longo tempo, o interruptor é girado para o contato com b. (a) Qual é a ca
No circuito da figura abaixo, a fem é igual a 6,00 V e a resistência interna é desprezível. A capacitância é igual a 1,50μ F e a resistência é igual a 2,00M Ω . A chave S ficou fechada por um longo te