Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 31.Problemas Adicionais - Ex. 70
Um circuito oscilante tem uma indutância de e uma capacitância de . Determine (a) a frequência angular e (b) o período de oscilação. (c) No instante , o capacitor é carregado com e a corrente é zero. Faça um esboço da carga do capacitor em função do tempo.
Passo 1
Bom, temos um circuito com um indutor e um capacitor. Para esse tipo de circuito, temos que
Usando e , temos que
Passo 2
A relação entre período e frequência é
Substituindo a resposta do item (a), obtemos
Passo 3
Devemos esboçar o gráfico da carga armazenada no capacitor em função do tempo. Sabemos que ela é dada por
Como em , temos que e , segue que e . Fazendo o gráfico:
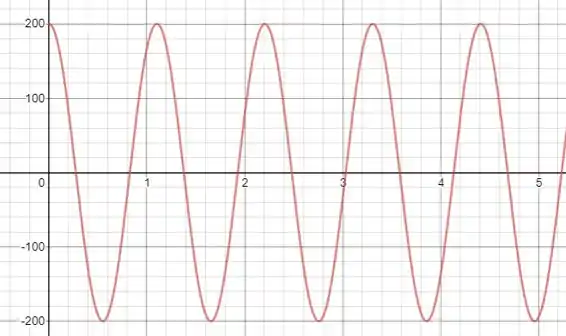
No gráfico, o tempo está em escala de , enquanto a carga está em .
Resposta
Exercícios de Livros Relacionados
43 - Uma corrente senoidal é dada por i = I cos ω t . A corrente obtida por um retificador de onda completa é indicada na Figura 31.3b. Sejam t 1 e t 2 os menores tempos positivos para os quais a co
54 - O circuito R-L-C em paralelo. Um resistor, um indutor e um capacitor são ligados em paralelo com uma fonte CA com amplitude de voltagem V e frequência angular ω . Suponha que a voltagem da fonte
53 - Um circuito R-L-C em série é conectado com uma fonte CA que possui uma amplitude de voltagem constante V e frequência angular variável ω . Mostre que a média temporal da energia armazenada no ind
52 - Um circuito R-L-C em série é conectado a uma fonte CA que possui uma amplitude de voltagem constante V e frequência angular variável ω . Usando os resultados do Problema 31.51, desenvolva uma exp
51 - Um circuito R-L-C em série é conectado a uma fonte CA com uma amplitude de tensão V constante e frequência angular variável ω . Mostre que a amplitude da corrente em função de ω é dada por I = V