Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 31.Problemas - Ex. 53

53 - Um circuito R-L-C em série é conectado com uma fonte CA que possui uma amplitude de voltagem constante V e frequência angular variável ω .

  1. Mostre que a média temporal da energia armazenada no indutor é U b = 1 4 L I 2 e a média temporal da energia armazenada no capacitor é U E = 1 4 C V 2 .
  2. Use os resultados dos problemas 31.51 e 31.52 para definir expressões para U b e U E em função de ω .
  3. Faça um gráfico de U b e U E em função de ω para V =   100   V , R =   200   Ω , L =   2,0   H e C =   0,50   μ F .
  4. Discuta o comportamento de U b e de U E nos limites ω = 0 e ω → ∞ . Para qual valor de ω obtemos U b = U E ? Qual é o significado desse valor de ω ?

Passo 1

L e t r a   A :

Ora, sabemos que a energia armazenada no indutor depende da corrente dessa forma aqui:

U b = 1 2 L i 2

Mas, nos lembrando de que a média temporal da corrente i é a correte eficaz I r m s ...

U b = 1 2 L I r m s 2

E que a corrente eficaz por sua vez se relaciona com a corrente de Pico...

U b = 1 2 L I 2 2 =

1 4 L I 2

Sacaca?

Passo 2

Podemos fazer o mesmo raciocínio para provar que...

U E = 1 4 C V 2

Ou seja, que na verdade a energia está definida em termos da tensão instantânea dessa forma aqui:

U E = 1 2 C v 2

Mas a média temporal de v é V r m s ...

U E = 1 2 C V r m s 2

E que V r m s está associado com o V de pico...

U E = 1 2 C V 2 2   →

U E = 1 4 C V 2

Passo 3

L e t r a   B :

Ora, sabemos dos problemas 51 e 52 que...

I = V R 2 + ω L - 1 ω C 2

E que...

V C = V ω C R 2 + ω L - 1 ω C 2  

Então...

U b = 1 4 L I 2         e             U E = 1 4 C V 2   →

U b = 1 4 L V R 2 + ω L - 1 ω C 2 2         e             U E = 1 4 C V ω C R 2 + ω L - 1 ω C 2 2   →

Simplificando eliminando esse quadrado...

U b = 1 4 R 2 + ω L - 1 ω C 2 L V 2         e             U E = 1 4 ω 2 C 2 C V 2 R 2 + ω L - 1 ω C 2       →

U b = L V 2 4 R 2 + ω L - 1 ω C 2         e             U E = 1 4 ω 2 C V 2 R 2 + ω L - 1 ω C 2       →

Passo 4

L e t r a   C :

Primeiramente vamos substituir os valores de V , L , C e R dados no item tanto em V L quanto em V C , se lembrando de que 0,5 μ F é 0,5 ⋅ 10 - 6 F ...

U b = 2 ⋅ 100 2 4 200 2 + ω 2 - 1 ω 0,5 ⋅ 10 - 6 2         e             U E = 1 4 ω 2 0,5 ⋅ 10 - 6 100 2 200 2 + ω 2 - 1 ω 0,5 ⋅ 10 - 6 2   →

U b = 20000 4 200 2 + ω 2 - 1 ω 0,5 ⋅ 10 - 6 2         e             U E = 1 2 ω 2 10 10 200 2 + ω 2 - 1 ω 0,5 ⋅ 10 - 6 2   →

Usando um aplicativo de construir gráficos e como o Winplot (aplicativo gratuito de construção de gráficos), vamos obter esses gráficos aqui: para o indutor U E (energia elétrica) com ω ...

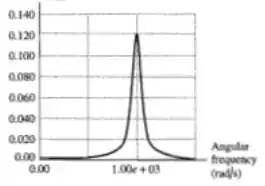
E já para U b (Energia Magnética) com ω ...

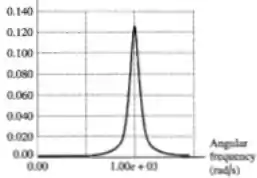
Passo 5

Quando a frequência é 0 , a energia magnética é 0 , já que o indutor é um curto nessa condição, enquanto que a energia armazenada no capacitor é a energia total dada pela tensão V :

U E = 1 4 C V 2

Já quando a frequência vai ao infinito...

U b = 20000 4 200 2 + ω 2 - 1 ω 0,5 ⋅ 10 - 6 2         e             U E = 1 2 ω 2 10 10 200 2 + ω 2 - 1 ω 0,5 ⋅ 10 - 6 2   →

Perceba que no caso da energia magnética salva no indutor vai a 0 , já que ômega está no denominador. Enquanto que a energia do capacitor, também vai a 0 por causa do ω 2 .

Passo 6

U b = U E

Acontece quando estamos na Ressonância...

ω = 1 L C = 1000 r a d / s

E essa é a frequência de ressonância!

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

67. No circuito indicado na Figura 30.27 , ε = 60,0V , R 1 = 40,0Ω , R 2 = 25,0Ω e L = 0,300H . A chave S está fechada para t = 0 . Logo depois de a chave ser fechada, ( a ) qual é a diferença de pote
A figura 29.47 indica um pequeno circuito dentro de outro maior, ambos repousando sobre a superfície de uma mesa. A chave está fechada no instante t = 0 com o capacitor inicialmente descarregado. Supo
76. Considere o circuito indicado na Figura 30.33 . Os elementos do circuito possuem os valores ε = 32,0V , L = 0,640H , C = 2,0μ F e R = 400Ω . A chave S é fechada para t = 0 . A corrente i 1 passa a
79. Considere o circuito indicado na Figura 30.35 . A chave S é fechada para t = 0 , produzindo uma corrente i 1 que passa através do ramo do indutor e uma corrente i 2 que passa através do ramo do ca
16. Repita o Exercício 31.14 com um circuito constituído somente pelo resistor e pelo capacitor em série. Para o item ( c ) , determine as amplitudes das tensões através do resistor e através do capac