Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 31.Problemas - Ex. 51

51 - Um circuito R-L-C em série é conectado a uma fonte CA com uma amplitude de tensão V constante e frequência angular variável ω .

  1. Mostre que a amplitude da corrente em função de ω é dada por

    2. I = V R 2 + ω L - 1 ω C 2

  2. Mostre que a potência média dissipada no resistor é

    3. P = V 2 R / 2 R 2 + ω L - 1 / ω C 2

  3. Mostre que I e P são ambos máximos quando ω = 1 / L C , ou seja, quando a frequência da fonte é igual à frequência de ressonância do circuito.
  4. Faça um gráfico de P em função de ω para V =   100   V , R = 200 Ω , L =   2,0   H e C   =   0,50   µ F . Compare o resultado com a curva indicada com o dístico de 200 Ω na Figura 31.19. Discuta o comportamento de I e de P nos limites ω = 0 e ω → ∞ .

Passo 1

L e t r a   A :

Poxa, podemos encontrar a corrente do circuito pela Lei de Ohm...

I = V Z

Onde Z é o módulo da impedância total do circuito formado pela série do Resistor com o indutor e o capacitor:

Z = R + j X l - j X c

Onde os X ’s representam as reatâncias que me função de ômega basicamente é...

Z = R + j ω L - j ω C     →

Z = R + j ω L - 1 ω C

O módulo de uma impedância complexa é o Pitágoras dos termos...

Z = R 2 + ω L - 1 ω C 2

Então, podemos concluir que a corrente no circuito R L C em série é...

I = V R 2 + ω L - 1 ω C 2

Passo 2

L e t r a   B :

Ora, a potência média dissipada pelo resistor é dada por...

P = 1 2 R I 2

Onde esse I é a amplitude de corrente encontrada anteriormente. A gente divide por 2 , pelo fato da corrente não ser a eficaz I q m . Então...

P = 1 2 R V R 2 + ω L - 1 ω C 2 2 =

1 2 R V 2 R 2 + ω L - 1 ω C 2

Então...

P = V 2 R / 2 R 2 + ω L - 1 / ω C 2

Passo 3

L e t r a   C :

Perceba que tanto a frequência quanto a corrente são os maiores possíveis quando o termo entre parênteses for 0 :

ω L - 1 ω C = 0     →

Então, isolando ômega...

ω L = 1 ω C     →

ω 2 = 1 L C →

ω = 1 L C

E esse ômega é a frequência angular de ressonância!

Passo 4

L e t r a   D :

Primeiramente, substituindo os valores dados em P ...

P = V 2 R 2 R 2 + ω L - 1 ω C 2   →

P = 100 2 ⋅ 200 2 200 2 + 2 ω - 1 0,5 ω ⋅ 10 - 6 2   →

Simplificando...

P = 1000000 20000 + 2 ω - 2000000 ω 2  

Usando um aplicativo de construir gráficos e como o Winplot (aplicativo gratuito de construção de gráficos), vamos obter esse gráfico aqui...

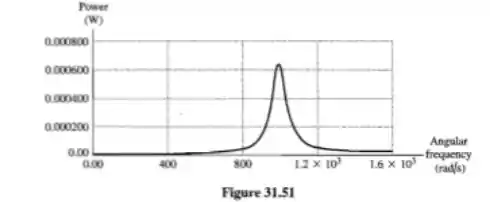
Veja pela fórmula que a medida que ômega vai a 0 :

P = 1000000 20000 + 2 ω - 2000000 ω 2  

O denominador vai para o infinito o que leva P para 0 (como mostrado no gráfico). Agora para quando ω vai ao infinito, o denominador continua indo para o infinito por causa do 2 ω o que leva P novamente para 0 . A corrente tem o mesmo padrão!

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

23. Em um circuito R - L - C em série, a voltagem eficaz através do resistor é igual a 30,0V , através do capacitor é igual a 90,0V e através do indutor é igual a 50,0V . Qual é a voltagem eficaz da f
24. Defina a reatância de um circuito R - L - C como X = X L - X C . ( a ) Mostre que X = 0 quando a frequência angular ω é igual à frequência angular da ressonância ω 0 . ( b ) Qual é o sinal de X pa
21. Análise de um circuito R - L - C . Você dispõe de um resistor de 200Ω , de um indutor de 0,400H , de um capacitor de 5,0μ F e uma fonte c a de frequência variável com amplitude de 3,0V . Todos ess
22. Um circuito R - L - C em série é construído com um resistor de 175Ω , um capacitor de 12,5μ F e um indutor de 8,0m H todos conectados através de uma fonte c a de frequência variável e uma amplitud
35- ( a ) Aplicando as equações ( 30.21 ) e ( 30.23 ) para um circuito L - C , escreva expressões para a energia armazenada em um capacitor em função do tempo e para a energia armazenada em um indutor