Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 26.1 - Ex. 38

O cloro tem dois isótopos estáveis, C l 35   e C l 37 . O gás de cloro, constituído de íons monovalentes, deve ser separado em suas componentes isotópicas usando um espectrômetro de massa. A intensidade do campo magnético no espectrômetro é 1,2   T . Qual é o valor mínimo da diferença de potencial através da qual estes íons devem ser acelerados para que a separação entre eles, depois de completarem uma trajetória semicircular, seja de 1,4   c m ?

Passo 1

SOMETHIN’ IN THE WAY SHE MOVES...opa, não te vi aqui perto, como você ta? Ah é mesmo, vou parar de enrolar, vamos para a questão!

Primeiramente, vamos analisar o diagrama abaixo que representa os caminhos de dois íons adentrando no campo magnético pela esquerda:

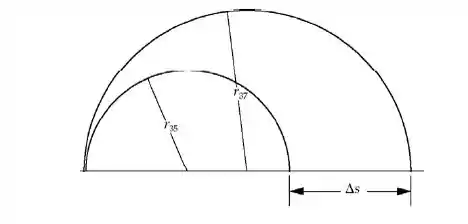
Podemos expressar a separação dos íons de cloro por ∆ s = 2 ( r 37 -   r 35 ) , agora precisamos determinar uma equação para os raios. Aplicando a segunda Lei de Newton em um íon no campo magnético, temos:

q   v   B = m v 2 r

r = m   v q   B

Agora determinaremos a velocidade do íon assim que ele entra no campo magnético, relacionando à diferença de potencial, no qual foi acelerado:

q   ∆ V = 1 2 m v 2

v = 2   q   ∆ V   m

Substituindo v na equação do raio:

r = m   q   B   2   q   ∆ V   m

r = 2   m   ∆ V   q   B 2

Passo 2

Utilizando a equação do raio para expressar os raios dos caminhos dos íons, temos:

r 35 = 2   m 35   ∆ V   q   B 2 e r 37 = 2   m 37   ∆ V   q   B 2

Agora, BORA APLICAR LOGO ISSO NA EQUAÇÃO DA SEPARAÇÃO:

∆ s = 2 2   m 37   ∆ V   q   B 2 -   2   m 35   ∆ V   q   B 2

∆ s = 2 1 B 2     ∆ V   q   ( m 37 -   m 35 )

∆ V = q B 2 ∆ s 2 2 2 m 37 -   m 35 2

Agora, substituiremos as variáveis pelos valores dados na questão:

∆ V = ( 1.602   x   10 - 19 C ) ( 1.2   T ) 2 1.4   c m 2 2 2 37 u -   35 u 2

∆ V = 5.65   x   10 - 24 C   .   T 2 .   m 2 ( 1.66   x   10 - 27 k g ) 37 -   35 2

∆ V = 0.12   M V

PRONTINHO, essa questão é das boas, é isso, É SÓ ISSO, muito bom ter sua companhia até aqui, volte mais vezes ;) BONS ESTUDOS!

Resposta

∆ V = 0.12   M V

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas cargas puntiformes iguais então, em algum instante, localizadas em 0,0 , 0 e em 0 , b , 0 . Ambas estão se movendo com rapidez v na direção + xc o n s i d e r ev ≪ c . Determine a razão entre a m
Um próton tem uma velocidade de 1,0 × 10 2 m sî+ 2,0 × 10 2 m sj î e está localizada no plano z = 0 em x = 3,0m ,y = 4,0m em um instante t = T . Determine o campo magnético no plano z = 0 em a x = 2,0
Um próton, um dêuteron e uma partícula alfa têm a mesma energia cinética. Eles estão se movendo em uma região com campo magnético uniforme que é perpendicular às suas velocidades. Sejam R p , R deR a
Um pequeno ímã em barra tem momento magnético μ → que faz um ângulo θ com o eixo x . O ímã está em uma região com um campo magnético não uniforme dado por B → = B x xî + B y yj î . Usando F x = - ∂ U
Como as propriedades das linhas de campo magnético são similares às propriedades das linhas de campo elétrico? Como elas são diferentes?