Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 26.Exercício - Ex. 5

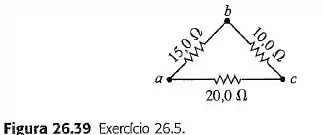
Uma combinação triangular de resistores é indicada na Figura 26.39. Qual é a corrente que essa combinação consumirá de uma bateria de 35,0 V, com resistencia interna desprezivel, quando ela é conectada através de (a) a b ; (b) b c ;   (c) a c ? (d) Caso a bateria tenha uma resistencia de 3,0   Ω , qual é a corrente que essa combinação consumirá, se a bateria for conectada através de b c ?

Passo 1

A resistência equivalente variará para as diferentes conexões, porque o paralelo em série

combinações variam e, portanto, a corrente varia.

Primeiro calcularemos a resistência equivalente usando as fórmulas paralelas em série, depois usaremos a lei de Ohm ( V = R I ) para encontrar a corrente.

Passo 2

  1. Vamos calcular a corrente que essa combinação consumirá de uma bateria de 35,0 V, com resistencia interna desprezivel, quando ela é conectada através de a b :

    2. 1 R = 1 15 Ω + 1 30 Ω

    Nos dá que:

    R = 10 Ω  

    I = V R = 35 V 10 Ω = 3,50   A

    Passo 3

  2. Vamos calcular a corrente que essa combinação consumirá de uma bateria de 35,0 V, com resistencia interna desprezivel, quando ela é conectada através de b c :

    3. 1 R = 1 10 Ω + 1 35 Ω

    Nos dá que:

    R = 7,78 Ω  

    I = V R = 35 V 7,78 Ω = 4,50   A

    Passo 4

  3. Vamos calcular a corrente que essa combinação consumirá de uma bateria de 35,0 V, com resistencia interna desprezivel, quando ela é conectada através de a c :

    4. 1 R = 1 20 Ω + 1 2 5 Ω

    Nos dá que:

    R = 11,11 8 Ω  

    I = V R = 35 V 11,11 Ω = 3 , 1 5   A

    Passo 5

  4. Da parte (b), a resistência do triângulo por si só é 7,78 Ω . Adicionando a resistência interna de 3.00 - Ω da bateria fornece uma resistência equivalente para o circuito de 10,78   Ω . Portanto, a corrente é I = 35,0 V 10,78 Ω = 3,25   A .

Faz uma grande diferença como o triângulo está conectado à bateria.

Resposta

  1. 3,50   A
  2. 4,50   A
  3. 3,15   A
  4. 3,25   A
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um equipamento possui um resistor X que se projeta de uma abertura lateral. Esse resistor é conectado a outros três resistores, como indica a Figura 26.38. Um ohmímetro conectado através de a e b regi
A potencia máxima especificada sobre o resistor é a maior potencia que pode ser dissipada no resistor, sem que ele atinja a temperatura demasiadamente elevada. (a) Se a potencia máxima que um resistor
Calcule a resistência equivalente do circuito indicado na Figura 26.43 e determine a corrente que passa em cada resistor. A bateria possui resistência interna desprezível.
Considere o circuito indicado na Figura 26.45. A corrente que passa pelo resistor de 6,0Ω é igual a 4,0Ω , no sentido indicado. Quais são as correntes que passam pelo resistores de 25,0Ω e 20,0Ω ?
Para o circuito na Figura 26.41, determine a leitura do amperímetro ideal, caso a bateria tivesse uma resistencia interna de 3,26Ω .