Começando com a situação de equilíbrio do problema , o sistema inteiro (balança, mola, copo e bola) agora está sujeito a uma aceleração para cima de magnitude (em um elevador, por exemplo.) Repita os diagramas de corpo livre e os cálculos do problema .
Passo 1
(a) O fato de que o sistema está acelerando para cima não muda as direções das forças, e nem implica na existência de novas forças, só exige que a resultante sobre todos os corpos seja vertical para cima.
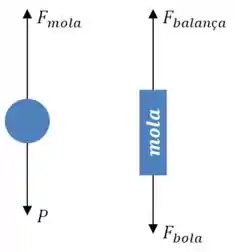
Então podemos manter o mesmo diagrama de antes, mas notando que agora a resultante é necessariamente vertical para cima.
Passo 2
(b) Antes nós consideramos que as forças verticais que agem sobre a bola estão em equilíbrio, mas agora vamos colocar uma resultante :
A força que a mola exerce sobre a bola pode ser calculada pela lei de Hooke:
E então o deslocamento da mola nesse instante é:
Passo 3
(c) E uma forma rápida de resolver essa questão é tomar o resultado do problema :
E usar o que chamamos de gravidade efetiva. Se o sistema acelera para cima com aceleração , nós podemos sem nenhum problema tratar ele como um sistema em que a aceleração da gravidade é:
E então é só substituir nas equações anteriores:
O que é um resultado bastante intuitivo, considerando que a medida da balança precisa aumentar quando o sistema acelera para cima.
Resposta
(a) Desenho.
(b) .
(c) A leitura da balança é .