Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 8.Problemas - Ex. 99

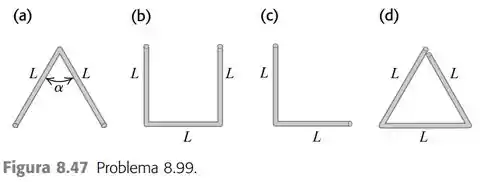
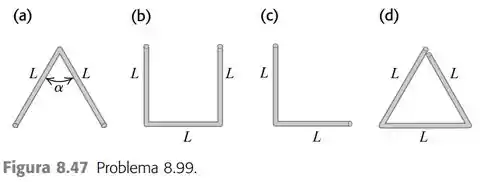
Os objetos da Figura 8.47 foram feitos com arames uniformes e dobrados nas formas indicadas. Ache a posição do centro de massa de cada um destes objetos.

Passo 1

Fala, galera! Beleza? Vamos resolver essa questão!

O enunciado pediu pra gente encontrar a posição do centro de massa de cada um dos objetos dados:

Vamos utilizar a E q . 8.28 para descrever o centro de massa das figuras acima. Assim sendo temos as coordenadas do centro de massa dadas por:

x c m = m 1 x 1 + m 2 x 2 + … + m n x n m 1 + m 2 + … + m n

e

y c m = m 1 y 1 + m 2 y 2 + … + m n y n m 1 + m 2 + … + m n

Assim, vamos considerar as massas m n genéricas e as posições x n relativas ao comprimento L e aos ângulos de cada figura e calcular cada coordenada.

Vamos lá!

Passo 2

a) Inicialmente podemos tentar resolver parte do problema por simetria. Analisando a figura (a), temos que ela é simétrica em uma dada direção, no caso podemos definir de x (eixo horizontal). Logo já podemos afirmar que o x c m é exatamente na metade das duas barras. Agora falta calcular o y c m :

y c m = m 1 L 2 cos ⁡ α 2 + m 2 L 2 cos ⁡ α 2 m 1 + m 2  

As posições y 1 e y 2 são tomadas dos centro de massa das barras. Outra coisa importante é que m 1 = m 2 = m

Logo temos que

y c m = 2 L 2 cos ⁡ α 2 2

y c m = L 2 cos ⁡ α 2

Passo 3

b) Seguindo a mesma logica no item (a), temos que o x _ c m para (b) é ainda na metade entre as duas barras oposta, ou seja, x c m = L 2 . Entretanto ainda precisando calcular para y c m :

y c m = m 1 L 2 + m 2 L 2 + m 3 ⋅ 0 m 1 + m 2 + m 3

y c m = 2 ⋅ L 2 3

y c m = L 3

Passo 4

c) Para o item (c) já não podemos usar a simetria do problema para nos ajudar. Mas podemos calcular.

x c m = m 1 L 2 m 1 + m 2 = L 4

y c m = m 2 L 2 m 1 + m 2 = L 4

Passo 5

d) Para esse ultimo item podemos usar novamente a simetria e indicar que o centro de massa para a posição x também se encontra na metade em L / 2 .

Para y temos temos que nos atentar que se trata de um triangulo equilátero. Logo temos que para calcular o ângulo de inclinação, vamos ter:

cos ��� β = 3 2 L L = 3 2

E substituindo na coordenada y c m junto com as outras variáveis, temos:

y c m = m 1 L 2 cos ⁡ β + m 2 L 2 cos ⁡ β + m 3 ⋅ 0 m 1 + m 2 + m 3

y c m = 2 3 ⋅ L 2 ⋅ 3 2

y c m = 3 L 6

Valeu, galera! Até a próxima! 😉

Resposta

  1. x c m = L   s e n α 2 e y c m =   L 2 cos ⁡ α 2
  2. x c m = L 2 e y c m =   L 3
  3. x c m = L 4 e y c m = L 4
  4. x c m = L 2 e y c m =   3 L 6
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O roteiro de um filme de ação requer que um pequeno carro de corrida (com uma massa de 1500k g e um comprimento de 3,0m ) acelere ao longo de uma barcaça ( com uma massa de 4000k g e um comprimento de
A Fig. 9-82 mostra uma placa quadrada uniforme de lado 6 d=6,0m da qual um pedaço quadrado de lado 2 d foi retirado. Quais são (a) a coordenadax e (b) a coordenada y do centro demassa da parte restant
Três massas pontuais de 2,0k g cada estão localizadas sobre o eixo x . Uma está sobre a origem, outra em x = 0,20m e outra em x = 0,50m . Encontre o centro de massa do sistema.
Em uma escavação arqueológica de fim de semana, você descobre um antigo martelo que consiste de uma pedra simétrica de 8,0k g presa na ponta de um pedaço de madeira uniforme de 2,5k g . Você mede as d
Três bolas, A , B e C , com massas 3,0k g , 1,0k g e 1,0k g , respectivamente, estão conectadas por hastes sem massa, como mostrado na figura. Quais são as coordenadas do centro de massa do sistema.