Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 8.Problemas - Ex. 34
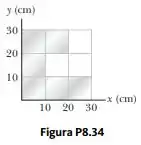
Um pedaço uniforme de folha de metal é moldado conforme mostrado na Figura P8.34. Calcule as coordenadas e do centro de massa da folha.
Passo 1
E aiii gente, tudo bem com vocês?
Vamos fazer uma questãozinha aqui?
Vem comigo!
Poderíamos analisar o objeto como nove quadrados, cada um representado por uma partícula de massa igual em seu centro. Mas vamos pensar na folha como composta de três seções, e considerar que a massa de cada seção está no centro geométrico dessa seção. Defina a massa por unidade de área como, e numere os retângulos como mostrado.
Podemos então calcular a massa e identifique o centro de massa de cada seção.
O centro de massa total está em um ponto definido pela equação vetorial:
Passo 2
Calculando:
Resposta
Exercícios de Livros Relacionados
Por simetria, localize o centro de massa de uma folha uniforme em forma de triângulo equilátero com lados de comprimento a . O triângulo tem um vértice no eixo y e os outros em ( - a 2 , 0 ) e ( + a 2
Duas hastes finas, uniformes e idênticas, cada uma de comprimento L , estão coladas nas extremidades uma da outra de forma que o ângulo na junção é de 90 ° . Determine a localização do centro de massa
Uma lata em forma de cilindro simétrico de massa M e altura H está cheia de água. A massa inicial da água é M , mesma massa da lata. Um pequeno buraco é feito no fundo da lata, e a água começa a escor
Encontre o centro de massa da folha uniforme de madeira na figura. Considere esse sistema como efetivamente composto de duas folhas, supondo que uma “massa negativa” para compensar o buraco. Portanto,
Repita a análise do problema 107 com um ângulo geral θ na junção, ao invés de 90 ° . Sua resposta concorda com o resultado específico para o problema 90 ° ? A sua resposta dá resultados plausíveis par