O módulo da velocidade de um projétil quando atinge a altura máxima é de . (a) Qual é o módulo da velocidade do projétil antes de atingir a altura máxima? (b) Qual é o módulo da velocidade do projétil depois de atingir a altura máxima? Se tomamos e como o ponto de altura máxima e consideramos como sentido positivo do eixo o sentido da velocidade do projétil nesse ponto, quais são (c) a coodenada e (d) a coordenada do projétil antes de atingir a tlura máxima e (e) a coordenada e (f) a coordenada do projétil depois de atingir a altura máxima?
Passo 1
A chave para entender essa questão é lembrar de duas coisas: a velocidade horizontal é constante, e a velocidade vertical varia com a aceleração da gravidade.
Então vamos fazer um desenho que mostre esses instantes antes e depois do projétil atingir a altura máxima, onde .
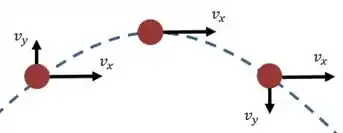
No ponto de altura máxima, o módulo da velocidade total é , então:
E para encontrar o módulo da velocidade vertical antes ou depois (dá no mesmo!), só precisamos considerar a aceleração da gravidade:
Aqui encontramos a velocidade depois do ponto máximo, mas o resultado teria o mesmo módulo se calculássemos a velocidade antes.
Então o módulo da velocidade nos dois instantes é:
Essa é a resposta dos itens (a) e (b).
Passo 2
Agora queremos encontrar as coordenadas em cada um dos instantes. Para isso vamos precisar de outro desenho:
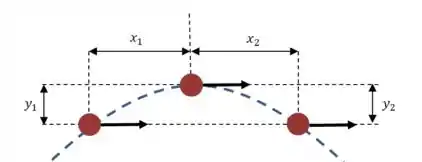
Mais uma vez só precisamos fazer a conta para um dos instantes, porque as coordenadas do outro terão exatamente o mesmo módulo.
Já que a velocidade horizontal do projétil é sempre igual a , qual é a distância percorrida durante ?
(c) Ou seja, se colocamos a origem do nosso sistema de coordenadas no ponto máximo, a coordenada do projétil antes passar pelo ponto máximo é:
Passo 3
(d) E agora, para calcular a distância vertical percorrida durante esse mesmo intervalo, vamos usar a seguinte fórmula:
Estamos analisando o projétil antes de atingir a altura máxima, ou seja, o projétil enquanto ainda está subindo. Por isso aparece o sinal negativo antes da aceleração , que está contrária à velocidade.
E nesse caso a velocidade inicial é :
Então a coordenada do projétil antes de atingir a altura máxima é:
Passo 4
(e) Agora, para encontrar as coordenadas do projétil depois de passar pelo ponto máximo, não precisamos fazer nenhuma conta nova.
É só perceber que as distância percorridas no intervalo de tempo de são as mesmas, tanto na vertical quanto na horizontal.
Olhando mais uma vez para o desenho, só precisamos ajustar os resultados ao nosso sistema de referência, onde a origem está sobre o ponto máximo:
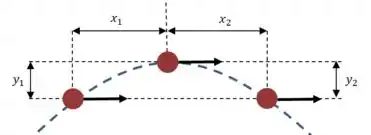
(e) Então, para a coordenada , temos:
(f) E para a coordenada , temos:
Resposta
(a) .
(b) .
(c) .
(d) .
(e) .
(f) .