Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 3.1 - Ex. 84

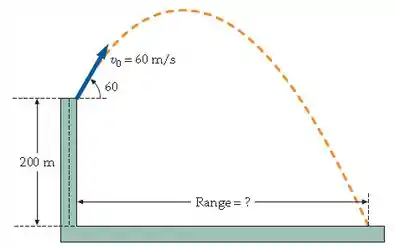
Um projétil é disparado do topo de uma colina de 200 m de altura, sobre um vale (Figura 3-36). Sua velocidade inicial é de 60 m/s, a 60° acima da horizontal. Onde o projeto cai? (Ignore a resistência do ar.)

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Nós queremos achar o alcance do projétil, que chamaremos de ∆ x .

Estamos diante de um lançamento obliquo, logo temos o movimento na direção horizontal, que é um movimento retilíneo uniforme e o movimento na direção vertical, que é um movimento uniformemente acelerado, no qual a aceleração é a gravidade, show?

Vamos começar analisando o movimento horizontal. Temos que:

∆ x = v 0 x t

Isso porque não há aceleração na horizontal.

Então:

∆ x = v 0 cos ⁡ 60 t

v o é dado na questão e cos ⁡ 60 é conhecido, logo:

∆ x = 60   .   1 2   .   t

∆ x = 30   t

Passo 2

Show de bola, agora precisamos achar o tempo pra podermos encontrar o alcance do projétil. Para isso vamos analisar o movimento vertical:

y = y 0 + v 0 y t + 1 2 a y t 2

Como v 0 y = v 0 sen ⁡ 60 e a y = - g , temos que:

y = y 0 + v 0 sen ⁡ 60 t - 1 2 g t 2

Substituindo os valores dados na questão:

0 = 200 + 60 . 3 2 t - 1 2 9,81 t 2

Resolvendo a equação, temos que:

t = 13,6   s

Passo 3

Tendo o tempo, achamos o alcance:

∆ x = 30 ⋅ 13,6

∆ x = 408   m

=)

Resposta

∆ x = 408   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma bola rola horizontalmente do alto de uma escada com uma velocidade de 1,52m / s . Os degraus têm 20,3c m de altura e 20,3c m de largura. Em que degrau a bola bate primeiro?
Uma pequena bola rola horizontalmente até a borda de uma mesa de 1,20m de altura e cai no chão. A bola chega ao chão a uma distância horizontal de 1, 52m da borda da mesa.(a) Por quanto tempo a bola f
Uma bola de futebol é chutada a partir do chão com uma velocidade inicial de 19,5m / s e um ângulo para cima de 45 ° . No mesmo instante, um jogador a 55m de distância na direção do chute, começa a co
O recorde atual de salto de motocicleta é 77,0   m , estabelecido por Jason Renie. Suponha que Renie tenha partido da rampa fazendo um ângulo de 12 ° com a horizontal e que as rampas de subida e de de
Um projétil é disparado horizontalmente de uma arma que está 45,0m acima de um terreno plano, saindo da arma com uma velocidade de 250m / s .(a) Por quanto tempo o projétil permanece no ar? (b) A que