Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 11.7 - Ex. 42
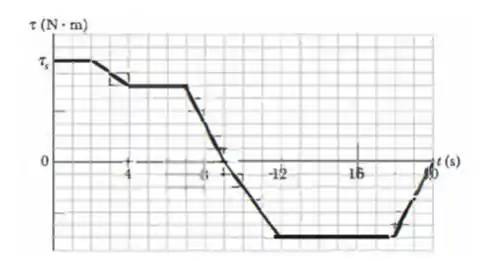
A figura abaixo mostra a variação com o tempo do torque que age sobre um disco inicialmente em repouso que pode girar como um carrossel em torno do centro. A escala do eixo é definida por . Qual é o momento angular do disco em relação ao eixo de rotação no instante
e
?
Passo 1
Olá pessoal, tudo bem? Vamos praticar um pouco o cálculo do momento angular?
Olha que sacada aqui! Você sabia que em um gráfico a área vai ser igual ao momento angular? Pois é! É esse conceito que vou usar aqui!
Cada quadradinho do eixo vertical vale e cada quadradinho do eixo horizontal vale , então agora é só calcular as áreas!
Ah! Lembra que área abaixo do eixo tem área negativa!
Passo 2
Para o intervalo de :
Passo 3
Para o intervalo até :
Resposta
Exercícios de Livros Relacionados
Uma particula de 1,8k g se move em um círculo de 3,4m de raio. Olhando de cima do plano de sua orbita, a particula está, inicialmente, se movendo no sentido horário. Chamando de positivo o sentido hor
Uma partícula, de massa m , viaja com uma velocidade constante v → ao longo de uma linha reta que dista b da origem O (figura 10-44). Seja d A a área varrida pelo vetor posição da partícula, em relaçã
Dois esquiadores no gelo, de massas 55k g e 85k g , dão-se as mãos e giram em torno de um eixo vertical que passa entre eles, completando uma volta a cada 2,5s . Seus centros de massa estão afastados
Uma roda de bicicleta, de raio igual a 28c m , está montada no meio de um eixo de 50c m de comprimento. O pneu e o aro pesam 30N . A roda é posta a girar a 12r e v / s , quando o eixo é colocado em po
O vetor posição de uma partícula de 3,0k g de massa é dado por r → = ( 4,0 ) i ^ + ( 3,0 t 2 ) j ^ , onde r → está em metros e t em segundos. Determine a quantidade de movimento angular e o torque res