Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 10.Problemas - Ex. 84

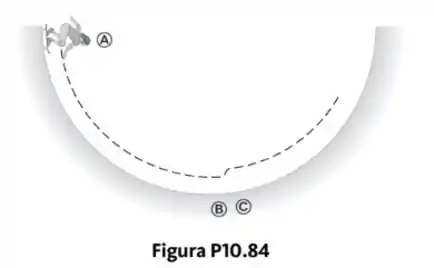
Um skatista com seu skate pode ser modelado como uma partícula de massa 76,0   k g , localizada em seu centro de massa, 0,500   m acima do chão. Como mostrado na Figura P10.84, o skatista parte do repouso em uma posição agachada na ponta do halfpipe (ponto A). Este forma a metade de um cilindro de raio 6,80   m com seu eixo horizontal. Em sua descida, o skatista desloca-se sem atrito e se mantém agachado, de modo que seu centro de massa se move por um quarto de um círculo.

  1. Encontre sua velocidade no fundo do halfpipe (ponto B).
  2. Encontre seu momento angular em torno do centro de curvatura neste ponto.
  3. Imediatamente após passar do ponto B, ele se levanta e ergue seus braços, elevando seu centro de gravidade para 0,950   m acima do concreto (ponto C). Explique por que seu momento angular é constante nessa manobra, ao passo que a energia cinética de seu corpo não é.
  4. Encontre sua velocidade imediatamente após ele se levantar.
  5. Quanta energia química nas pernas do skatista foi convertida em energia mecânica no sistema skatista-Terra quando ele se levantou?

Passo 1

E aiii gente, tudo bem com vocês?

Vamos fazer uma questãozinha aqui?

Vem comigo!

Letra a:

K + U g A = K + U 8 B 0 + m g y A = 1 2 m v B 2 + 0 v B = 2 g y A = 2 9.80 m s 2 6.30 m = 11.1 m / s

Passo 2

Letra b:

L = m v r = 76.0 k g 11.1 m s 6.30 m = 5.32 × 10 3 k g ⋅ m 2 s

Em sua direção ao longo do eixo do canal.

Passo 3

Letra c:

As rodas de seu skate impedem qualquer força tangencial de agir sobre ele. Então, nenhum torque sobre o eixo do canal atua nele e seu momento angular é constante. As pernas dele convertem energia química em energia mecânica. Eles trabalham para aumentar sua energia cinética. A força normal atua na direção para cima, perpendicular à direção do movimento do skatista.

Passo 4

Letra d:

L = m v r :

v = 5.32 × 10 3 k g ⋅ m 2 s 76.0 k g 5.85 m = 12.0 m s

Passo 5

Letra e:

K + U g B + U química   , B = K + U g C 1 2 ( 76.0 k g ) ( 11.1 m / s ) 2 + 0 + U química  

= 1 2 ( 76.0 k g ) ( 12.0 m / s ) 2 + ( 76.0 k g ) 9.80 m s 2 ( 0.450 m )

U química   = 5.44 k J - 4.69 k J + 335 J = 1.08 k J

Resposta

  1. 11.1 m s
  2. 5.32 × 10 3 k g ⋅ m 2 s
  3. As rodas de seu skate impedem qualquer força tangencial de agir sobre ele. Então, nenhum torque sobre o eixo do canal atua nele e seu momento angular é constante. As pernas dele convertem energia química em energia mecânica. Eles trabalham para aumentar sua energia cinética. A força normal atua na direção para cima, perpendicular à direção do movimento do skatista.
  4. 12.0 m s
  5. 1.08 k J
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Estime os valores inicais da rapidez com que se lança o patinador Timothy Goebel, da rapidez angular e da quantidade de movimento angular quando ele efetua um salto quádruplo (figura 10-41). Faça as s
Uma partícula de 2,0k g se move diretamente para o leste com uma rapidez constante de 4,5m / s , ao longo de uma linha oeste-leste. (a) Qual é sua quantidade de movimento angular (incluindo a orientaç
(a) Uma partícula, movendo-se com velocidade constante, tem quantidade de movimento angular zero em relação a um dado ponto. Use a definição de movimento angular para mostrar que, nestas condições, a
Você observa uma partícula de 2,0k g se movendo com uma rapidez constante de 3,5 m s no sentido horário em torno de um círculo de 4,0m de raio. (a) Qual é a quantidade de movimento angular da partícul
Uma moeda de 15g , com diâmetro de 1,5c m , rodopia a 10r e v / s em torno de um eixo vertical. Ela rodopia sobre a borda, com seu centro diretamente acima do ponto de contato com a mesa. Olhando de c