Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alaor Chaves- Ed: 1º - Capítulo 23.Exercícios e Problemas - Ex. 22

Considerando o sistema ilustrado na Figura 23.11, suponha que o disco tenha 10,0   c m de raio e que o campo magnético aplicado valha 2000   G . Se a resistência do circuito fechado for 300   Ω , (a) qual é o torque necessário para que o disco gire com frequência de 60   H z ? e (b) qual é a potência despendida para se manter o disco em rotação?

Passo 1

Eai galerinha, beleza?

Para entender esse problema você deve dar uma olhadinha especial na discussão feita na seção 23.7 do livro, na qual se deduz que a ddp entre o centro e a extremidade do disco é dada por

E = ω B R 2 2

Com isso aparece uma corrente de dentro para fora, como mostrada na figura a seguir:

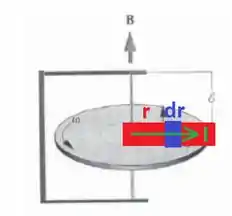
Vamos calcular o torque sobre essa faxinha pintada em vermelho. Para isso, lembramos que a força magnética sobre a porção d r será

d F = B I   d r

Com isso, o torque será dado por

d τ = r   d F = B I   r   d r

Fazendo a integral entre r = 0 e r = R nós achamos

τ = B I   ∫ 0 R r   d r = B I R 2 2

Passo 2

A corrente se relaciona com a fem por

E = R e s ⋅ I

Vou usar R e s para resistência para diferenciar do raio R . Com isso, temos

ω B R 2 2 = R e s ⋅ I → I = ω B R 2 2 R e s

Portanto, o torque fica

τ = ω B 2 R 4 4 R e s

Substituindo os valores temos que

τ = 2 π ⋅ 60 ⋅ 0,2 2 ⋅ 0,1 4 4 ⋅ 300

Fazendo as contas encontramos

τ = 1,26 ⋅ 10 - 6   N m

Passo 3

Para achar a potência usamos

P = E I = ω B R 2 2 ⋅ ω B R 2 2 R e s = ω τ

Logo,

P = 2 π ⋅ 60 ⋅ 1,26 ⋅ 10 - 6

Fazendo as continhas:

P = 4,74 ⋅ 10 - 4   W

Resposta

τ = 1,26 ⋅ 10 - 6   N m

P = 4,74 ⋅ 10 - 4   W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O fluxo magnético através de cinco faces de um dado é ϕ B = ± NW b , onde 1 ≤ N ≤ 5 é o número de pontos da face. O fluxo é positivo (para fora) se N é par e negativo (para dentro) se N é ímpar. Qual
Uma superfície gaussiana em forma de cilindro circular reto tem um raio de 12,0c m e um comprimento de 80,0c m . Em uma das bases existe um fluxo para dentro de 25μ W b . Na outra base existe um campo
Um capacitor de placas quadradas de lado L está sendo descarregado por uma corrente de 0,75 A. A figura 32-28 é uma vista frontal de uma das placas, do ponto de vista do interior do capacitor. A linha
O campo magnético induzido a 6,0m m do eixo central de um capacitor de placas circulares e paralelas é 2,0 × 10 - 7T . As placas têm 3,0m m de raio. Qual é a taxa de variação d E → / d t do campo elét
8 - O campo elétrico de uma onda eletromagnética senoidal obedece à equação E=–( 375V / m )s e n [ ( 5,97 ⋅10 15r a d / s ) t+( 1,99 ⋅ 10 7r a d / m ) x ] . Quais são a frequência, o comprimento de on