O campo magnético induzido a do eixo central de um capacitor de placas circulares e paralelas é . As placas têm de raio. Qual é a taxa de variação do campo elétrico entre as placas?

Lado esquerdo: vamos escolher uma amperiana circular de raio , porque queremos calcular o campo no espaço entre as placas do capacitor. O campo em todos os pontos da amperiana é tangente à curva, o que também acontece com o elemento de comprimento .

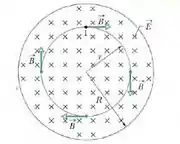
Assim, e são paralelos ou antiparalelos em todos os pontos da curva. Para simplificar os cálculos, vamos supor que sejam paralelos> Nesse caso, temos:

Devido a simetria circular das placas, podemos supor que o módulo de é o mesmo ao longo de toda a curva, podendo sair da integral e restando apenas a integral de . Essa, por sinal, é simplesmente perímetro da amperiana. Assim, o lado esquerdo da equação é .

Tranquilo até aqui? 😎

Lado direito: Vamos supor que o campo elétrico é uniforme na região entre as placas do capacitor e perpendicular às placas. Nesse caso, o fluxo elétrico através da amperiana é , onde é a parte da área envolvida pela amperiana que é atravessada pelo campo elétrico. Assim, o lado direito da euqação é .

Juntando os dois resultados, temos:

Legal, né? 👀

Nessa questão, nós queremos a taxa de variação do campo elétrico, ou seja, queremos achar o valor da ! Assim, vamos explicitar ele na equação encontrada no passo 3!

Fazendo as substituições dos valores

E aí, entendeu tudo? Responde Aí! 😁