Enunciado
Física - Moysés - Vol. 4 - Ed: 1º - Capítulo 6.Problemas - Ex. 2
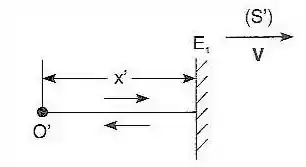
Considere agora a situação (fig.) em que o raio luminoso se reflete entre e um espelho à distância em (), na direção da velocidade. Calcule o tempo necessário para esse percurso de ida e volta no referencial (), levando em conta a dilatação dos intervalos de tempo. Mostre que isso permite obter a contração de Lorentz.
Passo 1
O tempo no referencial será:
O tempo no referencial pode ser escrito como sendo:
Precisamos encontrar .
Passo 2
Se o sistema de coordenadas não estivesse se movendo, teríamos:
Mas como o sistema tem velocidade , será:
Passo 3
Substituindo teremos:
Passo 4
Sabemos que a dilatação dos intervalos de tempo é:
Substituindo os intervalos de tempo, temos que:
que é a contração de Lorentz.
Resposta
Exercícios de Livros Relacionados
Um astronauta faz uma viagem de ida e volta em uma espaçonave, partindo da Terra, viajando em linha reta com velocidade constante durante seis meses e voltando ao ponto de partida da mesma forma e com
De volta para o futuro. Suponha que um astronauta é 20 anos mais velho que a filha. Depois de passar 4000 anos (no seu referencial) viajando pelo universo com velocidade constante, em uma viagem de id
Uma espaçonave interestelar viaja da Terra para um sistema estelar a 12 anos-luz de distância (conforme medido no referencial da Terra). A viagem dura 15 anos, conforme medido pelos relógios da nave.
O píon neutro π 0 tem uma massa de repouso de 135,0 MeV / c2. Esta partícula pode ser criada em uma colisão próton-próton: p + p → p + p + π0. Determine o limiar de energia cinética para a criação de
1 03 . Determine o parâmetro de velocidade para as seguintes velocidades: ( a ) o deslocamento de uma placa tectônica típica ( 2,5c m / a n o ) ; ( b ) a velocidade de deriva dos elétrons em um condut