Exercícios de Parâmetro de Velocidade e Fator de Lorentz - Lista de Exercícios Resolvida

De volta para o futuro. Suponha que um astronauta é 20 anos mais velho que a filha. Depois de passar 4000 anos (no seu referencial) viajando pelo universo com velocidade constante, em uma viagem de ida e volta, descobre, ao chegar à Terra, que está 20 anos mais moço que a filha.

Determine o parâmetro de velocidade da nave do astronauta em relação à Terra.

Uma espaçonave viaja com velocidade e o objetivo é concluir um percurso de .

Calcule o parâmetro de velocidade e o fator de Lorentz da nave.

Qual é o tempo medido para um observador na nave ao completar o percurso?

Qual é o tempo medido para um observador fixo fora da nave?

O comprimento de uma espaçonave em um certo referencial é a metade do comprimento de repouso. Com três algarismos significativos, qual é o parâmetro de velocidade da espaçonave no referencial do observador? Qual é a relação entre a rapidez da passagem do tempo no referencial da nave e no referencial do observador?

Um relógio está se movendo ao longo do eixo com uma velocidade de e indica o instante ao passar pela origem.

Calcule o fator de Lorentz do relógio.

Qual é a leitura do relógio ao passar pelo ponto ?

O referencial passa pelo referencial a uma velocidade ao longo da direção comum dos eixos e , como na figura abaixo.

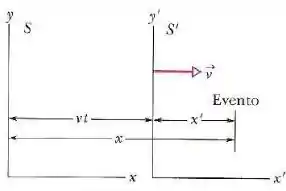
Um observador estacionário no referencial mede um certo intervalo de tempo com seu relógio de pulso. Um observador estacionário no referencial mede o intervalo correspondente .

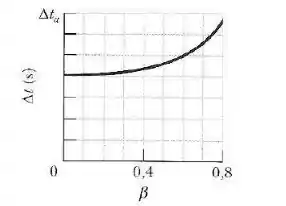
A figura abaixo mostra a variação de com o parâmetro de velocidade no intervalo . A escala do eixo vertical é definida por . Qual é o valor de para ?

Uma barra se move com velocidade constante ao longo do eixo do referencial , com a maior dimensão da barra paralela ao eixo . Um observador estacionário no referencial mede o comprimento da barra.

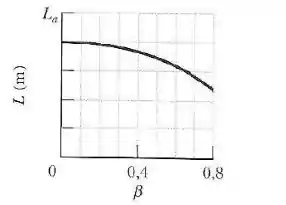
A figura abaixo mostra o valor de em função do parâmetro de velocidade para . A escala do eixo vertical é definida por . Qual é o valor de para ?

Faça a escolha correta e a justifique. Uma das afirmações abaixo NÃO é consequência das transformações de Lorentz:

(a ) Relógios em movimento possuem um ritmo maior do que relógios estacionários.

(b ) Objetos em movimento parecem mais curtos do que objetos estacionários.

(c ) Eventos simultâneos em um referencial inercial podem não ser simultâneos em outro referencial inercial.

(d ) Relógios em movimento possuem um ritmo menor do que relógios estacionários.

. O píon é uma partícula instável, com massa de repouso igual a , que é facilmente produzido nas interações de raios cósmicos atingindo a atmosfera e também em colisões produzidas em laboratório. Em um referencial , o píon é produzido na origem, se desloca com velocidade constante pelo eixo e se desintegra na posição após .

Qual é o tempo de vida próprio do píon?

Um evento ocorre no ponto sobre o eixo x e mais tarde um outro evento ocorre no ponto , tal que quando visto de S. Verifique matematicamente se é possível que estes dois eventos apareçam simultaneamente em um outro referencial S’, movendo-se paralelamente ao eixo x?

Em um universo onde a velocidade da luz vale , um corredor percorre certa distância em um intervalo de tempo , quando observado de um referencial . Ao terminar a corrida, o rolégio do corredor atribuirá ao percurso um intervalo de tempo . Sabe-se que o corredor manteve sua velocidade constante durante todo o percurso.

a) Calcule a velocidade do corredor em relação ao referencial .

b) Calcule a distância percorrida pelo corredor no referencial .

c) Qual o comprimento que o corredor, situado em , atribui ao trecho da pista percorrido por ele?