Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 3.1 - Ex. 78
Considere uma bola lançada do chão com uma rapidez inicial a um ângulo acima da horizontal. Chamando de a rapidez a uma altura h acima do chão, mostre que, para um dado valor de é independente de . (Ignore a resistência do ar.)
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
A figura abaixo retrata o movimento do enunciado:
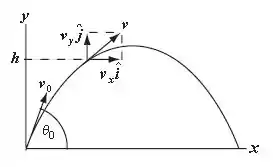
O problema nos pede para provar que a velocidade em qualquer ponto, não depende do ângulo de lançamento. Vamos analisar as componentes horizontal e vertical da velocidade.
Sabemos que:
Temos então que:
Portanto, é possível notar que a velocidade só depende da altura, da velocidade inicial e da aceleração da gravidade.
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Um projétil é lançado com urna velocidade inicial de 30m / s e um ângulo de 60 ° acima da horizontal. Determine (a) o módulo (b) o ângulo da velocidade 2,0s após o lançamento. (c) O ângulo do item (b)
O alcance de um projétil depende, não só de v 0 e θ 0 , mas também do valor g da aceleração em queda livre, que varia de lugar para lugar. Em 1936, Jesse Owens estabeleceu o recorde mundial de salto e
Uma bola de beisebol é golpeada junto ao chão. A bola atinge a altura máxima 3,0s após ter sido golpeada. Em seguida, 2,5s após ter atingido a altura máxima, a bola passa rente a um alambrado que está
Um projétil está sendo lançado do nível do chão, sem sofrer resistência do ar. Você quer evitar que ele penetre uma camada de inversão de temperatura na atmosfera a uma altura h sobre o solo. a) Qual
Um vaso de flores cai do peitoril de uma janela e passa pela janela de baixo. Despreze a resistência do ar. Ele leva 0,420s para passar por essa janela, cuja altura é igual a 1,90m . Qual é a distânci