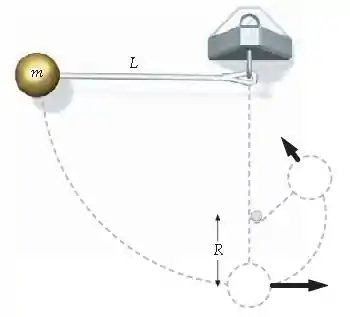
Um pêndulo consiste em uma pequena bola de massa presa a um fio de comprimento A bola é segurada lateralmente com o fio na horizontal (Figura 7-56). Então ela é largada do repouso. No ponto mais baixo da trajetória, o fio se prende a um pequeno prego, a uma distância acima desse ponto. Mostre que deve ser menor do que para que o fio permaneça tenso enquanto a bola completa uma volta inteira em torno do prego.

Oi pessoal, tudo bem? Vamos analisar essa questão.

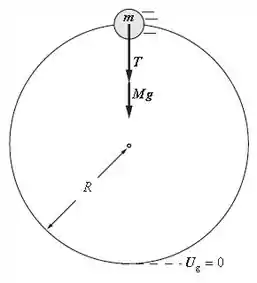
Bom pessoal, para que a bola complete a volta ao redor do prego a Força centrípeta deve ser maior que o Peso:

Analogamente, temos que a aceleração centrípeta deve ser maior que a aceleração da gravidade:

Usando conservação da energia mecânica para relacionar a energia cinética da bola no ponto mais baixo do loop com a energia potencial no topo, temos:

Resolvendo para , temos:

Substituindo na nossa condição do movimento, temos: