Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 36.Problemas adicionais - Ex. 98
Dois pontos estão separados por uma distância de . Se os pontos são vistos por um olho cuja pupila tem de diâmetro, a que distância do observador está o limite de resolução de Rayleigh? Suponha um comprimento de onda de para a luz.
Passo 1
Vamos começar calculando o limite de resolução angular, podemos fazer isso usando o critério de Rayleigh:
Passo 2
Agora vamos fazer um desenho que relacione isso com a posição do observador:
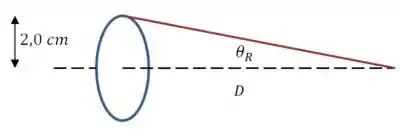
Pelo desenho, podemos escrever o seguinte:
Resposta
O observador está a de distância.
Exercícios de Livros Relacionados
A pupila do olho de uma pessoa tem um diâmetro de 5,0m m . De acordo com o critério de Rayleigh, qual deve ser a distância entre dois pequenos objetos para que estejam no limite da resolução quando se
Um astronauta a bordo do ônibus espacial afirma que pode resolver com dificudlade dois pontos sobre a superfície da Terra, 160k m abaixo. Calcule (a) a separação angular e (b) a separação linear dos p
Um satélite espião que está em órbita 160k m acima da superfície da Terra possui uma lente com uma distância focal de 3,6m e pode resolver objetos no solo com dimensões maiores que 30c m . Assim, por
Se uma pessoa olha para um objeto situado a 40m de distância, qual é a menor distância (perpendicular à linha de visão) que é capaz de resolver, de acordo com o critério de Rayleigh? Suponha que a pup
Em junho de 1985, o feixe de luz produzido por um laser na Estação Ótica da Força Aérea, em Maui, Havaí, foi refletido pelo ônibus espcial Discovery, que estava em órbita a uma altitude de 354k m . Se