Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 12.Exercícios e Problemas - Ex. 42
42. Considere os vetores e
a. Qual é o produto vetorial ?
b. Mostre os vetores , e em um sistema de coordenadas tridimensional.
Passo 1
Um jeito de calcular produto vetorial é usando determinante:
Onde a segunda linha representa o vetor e na última o vetor . Calculando o determinante normalmente...
Prontinho!
Passo 2
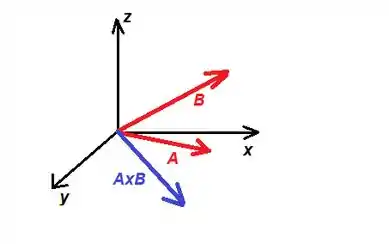
Resposta
Letra A:
Letra B:
Exercícios de Livros Relacionados
Um cilindro maciço e uniforme, de madeira, rola descendo um plano inclinado de um ângulo θ , sem deslizar. O coeficiente de atrito estático é μ . Determine (a) a aceleração do centro de massa do cilin
Uma esfera maciça e uniforme rola descendo um plano inclinado, sem deslizar. Se a aceleração linear do centro de massa da esfera é 0,20 g , qual é o ângulo de inclinação do plano com a horizontal?
Uma bola de basquete rola descendo um plano inclinado de um ângulo θ , sem deslizar. O coeficiente de atrito estático é μ . Trate a bola como uma casca esférica fina. Determine (a) a aceleração do cen
Um cilindro maciço e uniforme, de massa M e raio R , é colocado sobre uma barra de massa m , que, por sua vez, está sobre uma mesa horizontal sem atrito (figura 9-65). Se uma força F → é aplicada sobr
Uma bola de bilhar, inicialmente em repouso, recebe uma forte tacada. A força é horizontal e aplicada a uma distância 2 R 3 abaixo da linha diametral, como mostra a figura. A rapidez da bola imediatam