Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 11.Problemas - Ex. 83
Construtores de pirâmides. Construtores de pirâmides da antiguidade estão equilibrando uma laje de pedra homogênea e retangular, que está tombada a um ângulo acima do plano horizontal, usando uma corda (Figura 11.61). A corda é segurada por cinco trabalhadores que dividem igualmente a força.
a) Se, qual força cada trabalhador exerce sobre a corda?
b) À medida que aumenta, cada trabalhador tem que exercer mais ou menos força do que no item (a), supondo que eles não mudem o ângulo da corda? Por quê?
c) Qual o ângulo em que os trabalhadores não precisarão mais exercer nenhuma força para equilibrar a laje? O que ocorre, se exceder esse valor?
Passo 1
Para o equilíbrio já sabemos que . Vamos considerar a representação que envolve os ângulos
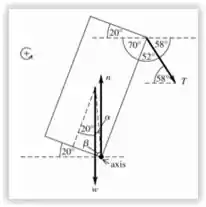
Calcunando a tangente, temos
Agora, vamos somar com os outros ângulos para acharmos o
Para a distância do eixo ao centro do bloco, aplicamos aquele velho Teorema do Tio Pit
Aplicaremos , para encontrarmos a força que cada trabalhador exerce sobre a corda
Passo 2
Para o item (b) temos que à medida que aumenta, o braço do momento para w diminui e o braço do momento para T aumenta, então o trabalhador precisa exercer menos força.
Passo 3
Para que os trabalhadores não exerçam nenhuma força para equilibrar a laje, o ângulo seria de quanto??
O valor de T tenderia a zero quando w passa pelo ponto de suporte, ficaria então
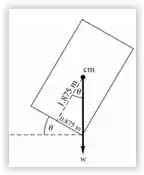
A tangente do ângulo já seria
Resposta
a)
b) o trabalhador precisa exercer menos força.
c)