Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 11.Problemas - Ex. 72
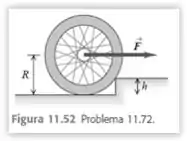
Você deseja fazer uma roda de bicicleta de massa m e raio R subir um desnível de altura h. Para fazer isso você aplica uma força horizontal (Figura 11.52). Qual é o menor módulo dessa
força para fazer a roda subir o desnível, quando a força é aplicada
a) no centro de gravidade da roda e
b) no topo da roda?
c) Em qual dos dois casos você precisa realizar uma força menor?
Passo 1
Fala aí! tudo certinho!
Nesse problema temos uma roda de massa e raio subindo um desnível de altura . Para fazer isso temos que aplicar uma força horizontal .
A partir daí queremos saber qual é o menor módulo dessa força para fazer a roda subir o desnível, quando a força é aplicada no centro de gravidade da roda e no topo da roda. Além disso temos que dizer em qual dos dois casos precisamos realizar uma força menor.
Tem ideia de como fazemos isso?
Vamos aplicar a segunda e a terceira lei de newton para o torque
Veja só!
Passo 2
Pela figura a força aplicada é , atuando horizontalmente.
Para a força peso, imaginemos um triangulo retângulo, logo
Se a força tem que ser mínima, os torques serão iguais, logo
Tranquilo até aqui?
Passo 3
Para o topo da roda, o torque será o mesmo, a diferença é que agora temos o diâmetro que é 2 vezes o raio, portanto,
E consequentemente
Show!
Passo 4
Para o item (c), percebemos que a menor força é na parte superior, pois nesse caso tem um braço de momento maior.
E aí! entendeu tudo? Responde Aí!
Resposta
- A menor força é na parte superior