Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 13.6 - Ex. 35
A mostra quatro partículas, todas de massa , que formam um quadrado de lado . Se é reduzido para , qual é a variação da energia potencial gravitacional do sistema?
Passo 1
Um corpo sofre a repulsão gravitacional de três corpos, sendo dois corpos que distam e outro que dista tal como podemos ver abaixo
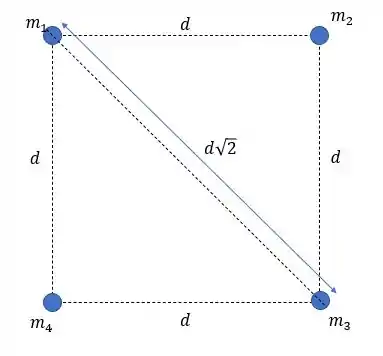
Portanto como a energia potencial gravitacional vale
Então:
Tem que garantir de pegar todas as distâncias.
Então se reduzirmos a distância em um terço nós temos uma nova energia potencial gravitacional igual a:
Com isso a variação de energia potencial será:
Passo 2
Aplicando os valores de e , então será:
Resposta
Exercícios de Livros Relacionados
14 . || Um foguete é lançado diretamente para cima a partir da superfície terrestre, com uma velocidade de 15.000m / s . Qual será sua velocidade quando estiver muito distante da Terra?
16 . || Você esteve visitando um planeta distante. Suas medições determinaram que a massa do planeta é duas vezes maior do que a da Terra, mas a aceleração de queda livre na sua superfície corresponde
12 . | Um astronauta na Terra consegue jogar uma bola para cima a uma altura de 15m . A que altura ele conseguiria jogar a bola em Marte?
15 . || Um ônibus espacial orbita o Sol à mesma distância que a Terra, mas do lado oposto ao Sol. Uma pequena sonda é lançada do ônibus. Qual é a velocidade mínima que a sonda necessita ter para escap
A FIGURA PD13.76 mostra uma partícula de massa m a uma distância x do centro de um cilindro muito fino, de massa M e comprimento L. A partícula se encontra fora do cilindro, de modo que xL/2. a. Calcu