Enunciado
Física - Moysés - Vol. 2 - Ed: 4º - Capítulo 3.Problemas - Ex. 4
Uma conta de massa enfiada num aro vertical fixo de raio , no qual desliza sem atrito, desloca-se em torno do ponto mais baixo, de tal forma que o ângulo permanece pequeno. Mostre que o movimento é harmônico simples e calcule o período.
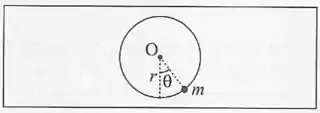
Passo 1
Vamos começar representando as forças que agem sobre o sistema:
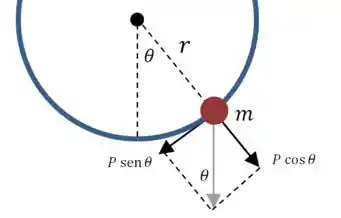
Agora vamos tentar montar uma equação que dê o ângulo em função do tempo.
Aplicando a segunda lei de Newton na direção tangencial, temos o seguinte:
E podemos escrever a aceleração na extremidade do círculo como:
Então:
Passo 2
Agora vamos resolver essa equação:
Segundo o enunciado, o ângulo permanece pequeno, então podemos usar a seguinte aproximação:
Essa é a EDO de um oscilador harmônico simples! A frequência angular desse oscilador é:
Então o período é:
Resposta
O movimento é harmônico simples e tem período .