Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 2- Ed: 14º - Capítulo 13.Exercícios - Ex. 52

Uma pequena esfera de massa m está presa a uma barra sem massa, de comprimento L, por meio de um pivô em sua extremidade superior, formando um pêndulo simples. O pêndulo é puxado lateralmente até um ângulo 8 com a vertical e a seguir é liberado a partir do repouso. (a) Desenhe um diagrama mostrando o pêndulo logo após o instante em que ele é liberado. Desenhe vetores representando as forças que atuam sobre a esfera e a aceleração da esfera. A precisão é importante! Nesse ponto, qual é a aceleração linear da esfera? (b) Repita o item (a) para o instante em que o pêndulo forma um ângulo (J/2 com a vertical. (c) Repita o item (a) para o instante em que o pêndulo está na direção vertical. Nesse ponto, qual é a velocidade linear da esfera?

Passo 1

Sabemos que:

a t a n = L α

a r a d = L ω 2

a = a t a n 2 + a r a d 2

Aplique a conservação de energia para calcular a velocidade em parte (c).

Logo após a esfera ser solta, ω = 0 e a r a d   =   0 . Quando a haste é vertical, a t a n   =   0

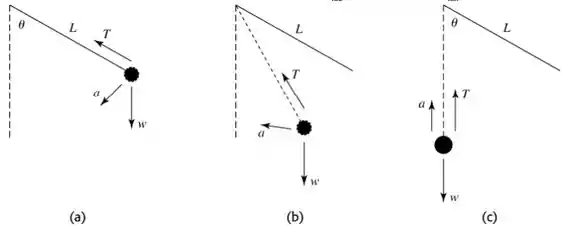
Figura 13.46

Passo 2

  1. As forças e aceleração são mostradas na Figura 13.46a. a r a d = 0   e   a t a n = g   s i n θ
  2. As forças e a aceleração são mostradas na Figura 13.46b.
  3. As forças e a aceleração são mostradas na Figura 13.46c. U i = K f dado m g L 1 - c o s Θ = 1 2 m v 2 e   v = 2 g L ( 1 - c o s Θ )

Resposta

Ver o desenvolvimento

Exercícios de Livros Relacionados

Suponha que os astronautas da primeira viagem a Marte levem consigo um pêndulo cujo período, na Terra, é de 1,50s . Verifica-se que seu período em Marte é de 2,45s . Qual é a aceleração de queda livre
A chave inglesa de 20c m de comprimento na FIGURA EX14.25 balança em torno de um orifício com período de 0,90s . Quando a chave está pendurada em uma mola com constante elástica de 360N / m , ela esti
57. Demonstre que a Equação 14.52, para freqüência angular de um pêndulo físico, recai na Equação 14.49 para o caso de um pêndulo simples formado por uma massa presa a uma mola.
56. A aceleração de queda livre na Terra varia de 9,78m / s 2 , no Equador, a 9,83m / s 2 , nos pólos, pelo fato de a Terra estar em rotação e também por ela não ser uma esfera perfeita. Um pêndulo cu
58. Uma das extremidades de uma haste de 15c m de comprimento é fixada por um pino. Uma bola de argila de 20g é presa à outra extremidade. Qual é o período se o bastão e a argila balançam como um pênd