Enunciado

Física - Halliday - Vol 4- Ed: 10º - Capítulo 37.Problemas adicionais - Ex. 67

Continuação do Problema 65. Suponha que o referencial C da Fig. 37-31 está se movendo em relação a um observador D (que não aparece na figura). (a) Mostre que

(b) Agora aplique este resultado geral a um caso particular. Três partículas se movem paralelamente a um único eixo no qual está estacionado um observador. Os sinais positivo e negativo indicam o sentido do movimento ao longo desse eixo. A partícula A se move relação à Partícula B com um parâmetro de velocidade . A partícula B se move em relação à partícula C com um parâmetro de velocidade . A partícula C se move em relação ao observador D com um parâmetro de velocidade . Qual é a velocidade da partícula A em relação ao observador D? (Este método de resolver o problema é muito mais rápido que usar a Eq. 37-29.)

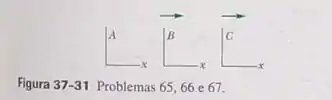
Passo 1

Para resolvermos esse problema vamos utilizar os resultados obtidos no exercício anterior para calcular todas as variáveis pedidas pelo enunciado.

Passo 2

Temos que pela simetria do problema, o cálculo feito para e serão respectivamente

Se substituirmos na segunda relação, teremos que

Passo 3

Utilizando a equação sugerida pelo enunciado, temos que

Se manipularmos essa equação, vamos chegar que

E que . Assim, temos que

Assim, utilizando a equação dada no item (a), temos que

E

Que fará com que a velocidade seja, por consequência,

Resposta

(b)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Outra abordagem para as transformações de velocidades. Na Fig. 37-31, os referenciais B e C se movem em relação ao referencial A na direção comum dos eixos x . Podemos representar os componentes x das

Continuação do Problema 65. Use o resultado do item (b) do Problema 65 para analisar o movimento ao longo de um único eixo na seguinte situação: o referencial A da Fig. 37-31 é associado a uma panícul

Na Fig.37-28a, a partícula P se move paralelamente aos eixos x e x ' dos referenciais S e S ' , com uma certa velocidade em relação ao referencial S . O referencial S ' se move paralelamente ao eixo x

Uma espaçonave em repouso em um certo referencial S sofre um incremento de velocidade de 0,50 ⋅ c . Em seguida, a nave sofre um incremento de 0,50c em relação ao novo referencial de repouso. O process

Uma partícula proveniente do espaço sideral se aproxima da Terra ao longo do eixo de rotação do planeta com uma velocidade de 0,80c , vido do note, e a outra partícula se aproxima com uma velocidade d