Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Halliday - Vol 4- Ed: 10º - Capítulo 37.Problemas adicionais - Ex. 62

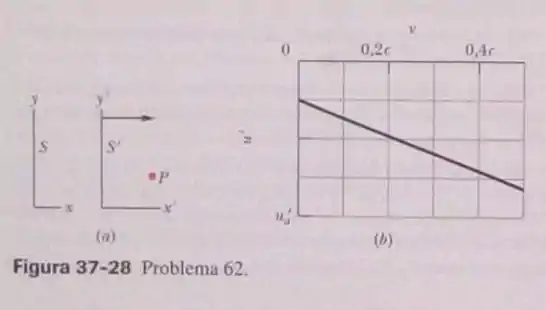
Na Fig.37-28a, a partícula P se move paralelamente aos eixos x e x ' dos referenciais S e S ' , com uma certa velocidade em relação ao referencial S . O referencial S ' se move paralelamente ao eixo x do referencial S com velocidade v . A Fig. 37-28b mostra a velocidade u ' da partícula em relação ao referencial S ' para 0 ≤ v ≤ 0,5 ⋅ c . A escala do eixo vertical é definida por u a ' = - 0,800 ⋅ c . Determine o valor de u ' (a) para v = 0,80 ⋅ c e (b) para v → c .

Passo 1

Para resolvermos esse problema vamos utilizar a equação para velocidade relativa entre os referenciais para descobrirmos as velocidades u ' para cada caso de v .

Passo 2

  1. Observando o gráfico dado pelo exercício, supondo que ambas as velocidades estão na mesma escala, temos que quando v = 0 , u ' = - 0,20 ⋅ c . Assim, utilizando a seguinte equação

    2. u ' = u - v 1 - u ⋅ v c 2

    E substituindo o valor de v para esse caso, que será v = 0,80 ⋅ c , teremos que

    u ' = - 0,20 ⋅ c - 0,80 ⋅ c 1 + 0,20 ⋅ 0,80 ⋅ c 2 c 2 = - 0,86 ⋅ c

    Passo 3

  2. Utilizando a mesma equação do item anterior, temos que para v = c , u ' será

u ' = - 0,20 ⋅ c - c 1 + 0,20 ⋅ c 2 c 2 = - c

Como esperado, já que pelos postulados da relatividade é impossível ter uma acima da velocidade da luz.

Resposta

a) u ' = - 0,86 ⋅ c

b) u ' = - c

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma espaçonave da Armada Imperial se desloca com velocidade elevada em relação ao planeta Arrakis e dispara um foguete na direção do planeta com uma velocidade de 0,920c em relação à espaçonave. Um ob
Duas partículas são produzidas em um acelerador de partículas de alta energias e se afastam em sentidos opostos. A velocidade de uma das partículas, medida no laboratório, é igual a 0,0650c , e a velo
Duas partículas provenientes de um acelerador de partículas de alta energia se aproximam frontalmente com uma velocidade relativa igual a 0,9520c medida no laboratório. Qual é o módulo da velocidade c
Em uma experiência, duas partículas em um acelerador de partículas de alta energia se aproximam uma da outra em sentidos opostos com uma velocidade relativa de 0,890 c. Ambas as partícula se deslocam
Uma nave do planeta Tatooine está tentando alcançar um cruzador da Federação do Comércio. Em relação a um observador em Tatooine, o cruzador está se afastando do planeta com uma velocidade de 0,600 c