Enunciado
Física - Moysés - Vol. 2 - Ed: 4º - Capítulo 5.Problemas - Ex. 8
Uma corda de comprimento está distendida, com uma extremidade presa a um suporte e a outra extremidade livre. (a) Ache as frequências dos modos normais de vibração da corda. (b) Desenhe a forma da corda associada aos três modos de vibração mais baixos (em ordem de frequência crescente). A velocidade de ondas na corda é .
Passo 1
(a) Podemos escrever qualquer modo normal de vibração da corda como:
Substituindo isso na equação de onda, podemos encontrar uma equação diferencial que a função sempre tem que obedecer:
Onde . Nesse caso a solução geral para é:
Para determinar essas constantes todas, vamos usar as duas condições de contorno que foram dadas no enunciado:
A primeira diz que uma das extremidades está fixa o tempo todo, e a segunda diz que a tangente à corda na extremidade sempre fica na horizontal.
Obs.: Essa segunda condição pode parecer mais difícil de entender, mas é sempre válida para uma corda com extremidade livre, desde que não haja nenhuma força transversal.
Passo 2
Agora vamos aplicar essas condições:
A única solução razoável para essa equação é:
Então:
Agora vamos aplicar a segunda condição:
Mais uma vez, a única solução que faz sentido é:
Como , ficamos com a seguinte solução:
E podemos relacionar com a frequência do modo normal:
Passo 3
(b) Agora vamos fazer os gráficos dos três primeiros modos normais dessa corda.
Já que a corda tem comprimento fixo, e sabemos que são modos normais, basta determinar o comprimento de onda para poder fazer o gráfico.
Uma das fórmulas para o comprimento de onda é:
Aproveitando a mesma relação de antes para :
Passo 4
Queremos fazer os gráficos em ordem crescente de frequência. Isso significa que vamos começar com o maior comprimento de onda:
Para temos:
Isso quer dizer que a corda inteira vai formar um quarto de comprimento de onda:
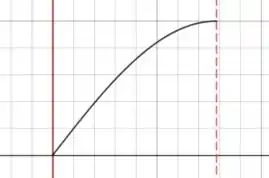
Nesses desenhos a distância entre as duas retas vermelhas é sempre igual a .
Para :
E para :
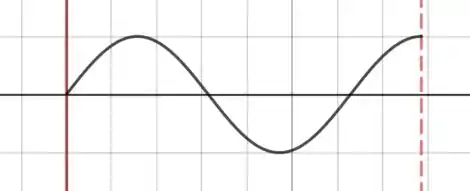
Resposta
(a) , com .
(b) Ver figuras.