Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 15.4 - Ex. 52
O cubo de 3,00 kg na Fig. 15-45 tem de aresta e está montado em um eixo que passa pelo centro. Uma mola () liga o vértice superior do cubo a uma parede rígida. Inicialmente, a mola está relaxada. Se o cubo é girado de 3º e liberado, qual é o período do MHS resultante?
Passo 1
Show de bolinhas galera, antes da gente achar o período T, vamos calcular a energia cinética máxima. Ela é igual a máxima energia potencial, logo:
O deslocamento a gente descobre fazendo um triângulo retângulo que pega os pontos centro do cubo, vértice superior antes do giro de 3° e o vértice superior após o giro de 3º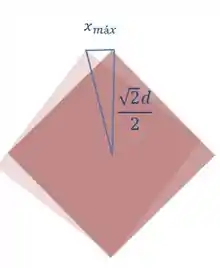
Sendo assim, podemos escrever que:
Logo:
Sendo assim, teremos:
Substituindo os valores, teremos:
E igualando essa energia potencial máxima com a energia cinética de rotação máxima (isso mesmo, de rotação, afinal esse cubo vai começar a rodar).
A máxima velocidade angular do cubo é (não confundir com a velocidade angular de oscilação!).
Passo 2
Achando , a gente consegue diretamente achar a frequência de oscilação do cubo, e a partir dela achar o período T.
Antes disso, vamos calcular o momento de inércia do cubo (esse momento de inércia é tabelado.)
Substituindo na equação 1 e isolando , a gente tem:
O próximo passo agora é relacionar com . Esta relação pode ser encontrada fazendo a derivada da posição :
Derivando:
E o valor que acompanha a senóide é a amplitude, por isso:
E o ângulo máximo da oscilação vai ser o ângulo do qual o cubo começou as suas oscilações, que é exatamente o ângulo que ele foi girado antes de ser solto:
Portanto, teremos:
Tendo o valor da frequência angular de oscilação, a gente consegue calcular o período T de oscilação.
