Um bloco retangular, com faces de largura e comprimento , é suspenso por uma barra fina que passa por um pequeno furo no interior do bloco e colocado para oscilar como um pêndulo, com uma amplitude suficientemente pequena para que se trate de um MHS. A Fig. 15-43 mostra uma possível posição do furo, a uma distância do centro do bloco, sobre a reta que liga o centro a um dos vértices. (a) Plote o período em função da distância de modo que o mínimo da curva fique evidente. (b) O mínimo acontece para que valor de ? Na realidade, exite um lugar geométrico em torno do centro do bloco para qual o período de oscilação possui o mesmo valor mínimo. (c) Qual é a forma desse lugar geométrico?
Passo 1
Conforma a o ponto de articulação muda, a distribuição de massa vai mudando também, e com isso o período de oscilação. Vamos escreve a equação para o período de um corpo.
onde é o momento de inércia e é a distância do ponto de articulação até o centro de massa. No nosso caso,
O momento de inércia de um retângulo é dado pela equação abaixo
Usando o teorema dos eixos paralelos e substituindo na equação 1, a gente tem
Beleza, já temos em função de . Substituindo os valores de e que o problema forneceu, a gente consegue plotar o gráfico
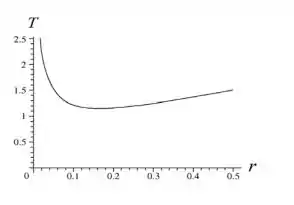
Passo 2
Pra achar o valor do mínimo, basta derivar a equação com relação a e igualar a zero.
Passo 3
A direção deste ponto não é importa. Só o que importa é a distância dele ao centro de massa. Assim, o lugar geométrico é um círculo de raio 0,16 m localizado no centro de massa do retângulo.
Resposta
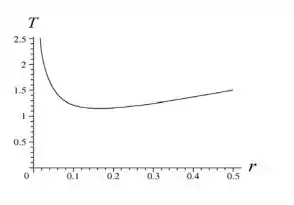 (a)
(a)
(b)
(c) O lugar geométrico é um círculo de raio 0,16 m localizado no centro de massa do retângulo.