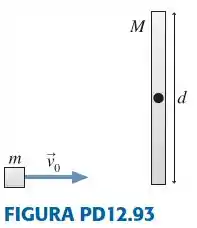
|| Um cubo de massa m desliza sem atrito com velocidade . Ele, então, sofre uma colisão perfeitamente elástica com a extremidade inferior de uma haste de comprimento d e massa . A haste está presa a um eixo livre de atrito que passa por seu centro e, inicialmente, encontra-se na posição vertical, em repouso. Qual será a velocidade do cubo - módulo e orientação - após a colisão?

Usando conservação da Energia():

Pela , nós podemos rescrever :

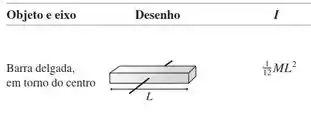
E o também há essa fórmula útil entre e :

Então reescrevendo a com o novo e:

Dá uma equação de , para . Aplicando Bhaskara:

Ficamos só com para direita, por que o