Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 5.1 - Ex. 94

Uma curva de 150   m de raio é inclinada por um ângulo de 10 ° . Um carro de 800   k g passa pela curva a 85   k m / h sem derrapar. Negligencie os efeitos do arrasto do ar e do atrito de rolamento. Encontre (a) A força normal exercida pelo pavimento sobre os pneus., (b) a força de atrito exercida pelo pavimento sobre os pneus, (c) o coeficiente de atrito estático mínimo entre o pavimento e os pneus.

Passo 1

Vamos desenhar o diagrama das forças:

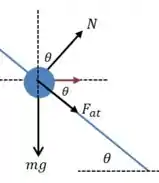
A seta vermelha aponta na direção da resultante centrípeta. Vamos somar as forças que agem nessa direção:

∑ F c = N sen ⁡ θ + F a t cos ⁡ θ = m v 2 r

E na direção vertical

∑ F y = N cos ⁡ θ - F a t sen ⁡ θ - m g = 0

Então ficamos com o seguinte sistema:

N sen ⁡ θ + F a t cos ⁡ θ = m v 2 r N cos ⁡ θ - F a t sen ⁡ θ = m g

Passo 2

Primeiro queremos resolver esse sistema para encontrar N . Vamos multiplicar a equação de cima por sen ⁡ θ , e a de baixo por cos ⁡ θ :

N sen 2 ⁡ θ + F a t cos ⁡ θ sen ⁡ θ = m v 2 r sen ⁡ θ N cos 2 ⁡ θ - F a t sen ⁡ θ cos ⁡ θ = m g cos ⁡ θ

Agora vamos somar as duas equações, e fazendo isso o termo com F a t vai sumir:

N sen 2 ⁡ θ + cos 2 ⁡ θ = m v 2 r sen ⁡ θ + m g cos ⁡ θ

N = m v 2 r sen ⁡ θ + m g cos ⁡ θ

Agora é só substituir os valores para calcular a normal ( v = 85 k m h = 23,6 m s ).

N = 800 23,6 2 ( 150 ) sen ⁡ 10 ° + ( 800 ) ( 9,81 ) ( cos ⁡ 10 ° )

N = 8,245   k N ≅ 8,2   k N

Passo 3

(b) Agora que sabemos o valor de N , podemos substituir em qualquer uma das equações para encontrar F a t :

N cos ⁡ θ - F a t sen ⁡ θ = m g

F a t = N cos ⁡ θ - m g sen ⁡ θ

F a t = 8245 cos ⁡ 10 ° - ( 800 ) ( 9,81 ) sen ⁡ 10 °

F a t = 1,564   k N ≅ 1,6   k N

Passo 4

(c) Vamos lembrar da definição da força de atrito máxima que a superfície pode fornecer:

F a t = μ e s t N

Onde μ e s t é o coeficiente de atrito estático:

μ e s t = F a t N

μ e s t = 1564 8245 = 0,19

Resposta

(a) N = 8,2   k N .

(b) F a t = 1,6   k N .

(c) μ = 0,19 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Suponha que a Eq. 6-14 forneça a força de arrasto a que estão sujeitos um piloto e o assento de ejeção imediatamente após terem sido ejetados de um avião voando horizontalmente a 1300k m / h . Suponha
Calcule a razão entre a força de arrasto experimentada por um avião a jato voando a 1000k m / h a uma altitude de 10k m e a força de arrasto experimentada por um avião a hélice voando a metade d
Ao descer uma encosta, um esquiador é freado pela força de arrasto que o ar exerce sobre o seu corpo e pela força de atrito cinético que a neve exerce sobre os esquis. (a) Suponha que o ângulo da enco
Continuação do Problema 8. Suponha agora que a Eq. 6-14 forneça o módulo da força de arrasto que age sobre uma pedra típica de 20k g , que apresenta ao vento uma área de seção reta vertical de 0,040m
Continuação dos Problemas 8 e 37. Outra explicação é que as pedras se movem apenas quando a água que cai na região durante uma tempestade congela, formando uma fina camada de gelo. As pedras ficam pre