Uma partícula se move com rapidez constante em um círculo de raio . Ele leva para completar cada revolução. (a) Desenhe o caminho da partícula em escala, e indique a posição da partícula em intervalos de . (b) Esboce os vetores de deslocamento para cada intervalo. (c) Graficamente, encontre a magnitude da mudança da velocidade média para dois intervalos consecutivos de um segundo. Compare , medido dessa forma, com a magnitude da aceleração instantânea computada por .
Passo 1
(a) Se a partícula atravessa um círculo inteiro em , isso quer dizer que a cada segundo ela percorre o seguinte arco:
Então vamos desenhar isso em um círculo de raio :
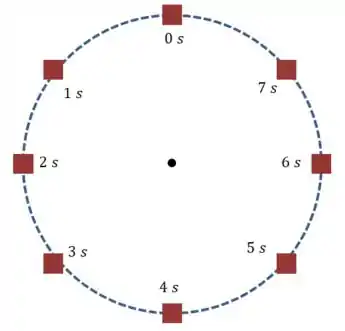
Passo 2
(b) Agora vamos esboçar os vetores de deslocamento:
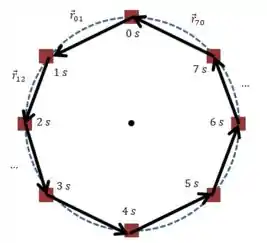
Passo 3
(c) Vamos lembrar da definição da velocidade média:
Como encontrar o módulo de ? Podemos usar uma fórmula geral para um segmento que une dois pontos sobre uma circunferência:
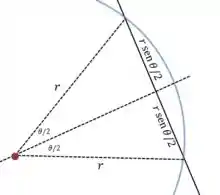
No nosso caso o ângulo é , e , então:
Ou seja:
Mas nosso objetivo final é calcular , como já vimos que os dois vetores são paralelos (e a rapidez é constante, assim como o raio ), podemos calcular os módulos usando a mesma lógica:
E então:
Agora já podemos escrever uma expressão para :
E substituindo os valores numéricos, podemos obter uma estimativa para a aceleração instantânea :
Passo 4
Vamos agora calcular a aceleração instantânea usando a fórmula:
E reescrevendo a rapidez :
Que é bastante próximo do resultado anterior:
Resposta
(a) Desenho.
(b) Desenho.
(c) Sendo a aceleração medida graficamente e medida pela definição, encontramos .