Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 3.1 - Ex. 115
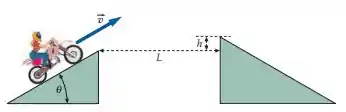
Darlene é uma motociclista de circo. Como clímax de seu show, ela larga de uma rampa inclinada de , salta um fosso de largura e pousa em uma rampa mais elevada (altura ) do outro lado. (a) Para uma dada altura h, encontre a mínima rapidez de largada necessária para ela realizar o salto com sucesso. (b) Quanto vale para , e ? Mostre que, independente da rapidez de largada, a altura máxima da plataforma é . Interprete fisicamente este resultado. (Despreze a resistência do ar e trate a motoqueira e a moto como se fossem um única partícula)
Passo 1
E aí pessoal, beleza? Vamos lá resolver esse problema. A gente quer descobrir a mínima velocidade necessária de Darlene quando ela sai da primeira rampa.
Basicamente, a gente quer saber a velocidade inicial mínima para que esse salto aconteça. Podemos aproximar esse salto como um lançamento de projetil. Então aqui a gente vai usar as expressões que regem esse movimento e achar a velocidade inicial que torna o movimento possível.
Primeiro, adote um sistema de coordenadas adequado. Vamos adotar o padrão que é positivo no sentido crescente de x e y.
Darlene deve imprimir uma certa velocidade inicial para conseguir realizar a acrobacia. Então vamos descobrir essa velocidade.
Para o movimento de projetil, o movimento em cada direção é idependente. Vamos começar olhando a direção horizontal. Nela, temos velocidade constante, e vale a equação:
Onde, é a distância percorrida horizontalmente. Pela figura, essa distância precisa ser o vão entre as rampas, que vale . A posição inicial vai ser zero porque nossa origem está na ponta da primeira rampa.
E a velocidade é a componente horizontal da velocidade inicial mínima da moto, que pode ser escrita como:
Logo, nossa equação fica:
Passo 2
Agora vamos avaliar o movimento vertical. Para ele, vale a seguinte equação:
A gravidade aparece com sinal de menos porque nosso eixo é positivo para cima. é a altura em , ou seja, na ponto da segunda rampa. Colocando a origem do eixo na ponta da primeira rampa, temos que . E assim a posição inicial é nula .
Já a velocidade inicial na direção vai ser a componente vertical de , dada por
Substituindo essas coisas na nossa equação:
Passo 3
Percebe que a gente ficou com duas equações que usam os dados do problema:
Percebe que a gente quer encontrar , e a gente conhece (da figura do enunciado) todas as letras que aparecem nessas equações, menos o tempo . Então vamos fazer ele sumir.
Como? A gente pode isolar ele na equação de cima e substituir na equação de baixo:
Subsituindo na segunda equação que a gente achou:
Isolando :
Prontinho!
Obs: no gabarito aparece um dentro da raiz, mas esse é um errinho deles, tá bem?
Passo 4
b) Agora queremos saber em valor a velocidade mínima que deve ser imprimida para as seguintes condições:
É só a gente usar a nossa equação encontrada antes com esses dados:
Substituindo:
Passo 5
c) Agora devemos mostrar que independente da velocidade inicial. A altura máxima da plataforma deve ser
Observe a equação que encontramos para a velocidade mínima inicial que deve ser imprimida, e analíse a parte que está dentro da raiz. Temos que, para que exista:
Pois o valor dentro da raíz não pode ser negativo (condição de existência de raízes pares). Como a gravidade não é negativa podemos dizer que:
Logo:
Passo 6
Para entender o que ele significa fisicamente, podemos isolar a tangente:
Percebe pela figura, que a gente tem esse triângulo:
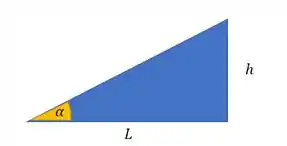
A tangente de é
Percebe que isso aparece na nossa desigualdade. Vamos substituir:
Como e são inclinações menores que , isso implica em
E como podemos interpretar isso? Quer dizer que a inclinação da rampa precisa ser maior do que a inclinação desse triângulo azul que a gente desenhou, para que a moto consiga subir o suficiente para atravessar o vão, já que é uma relação entre e o vão.
Resposta
O valor dentro da raíz quadrada não pode ser negativo, portanto deve se respeitar que .