Enunciado
Física - Moysés - Vol. 4 - Ed: 1º - Capítulo 5.Problemas - Ex. 4
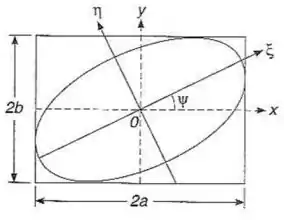
Demonstre, para o caso geral de polarização elíptica (5.29), que o ângulo entre o eixo maior da elipse de polarização e o eixo é dado por (fig.)
Onde
Passo 1
Bom, vamos dar uma olhada nas equações de polarização que o enunciado mencionou:
Onde . Beleza, como a gente relaciona isso com uma forma geométrica? O livro faz essa demonstração e até dá uma fórmula. Vamos repassar isso bem rápido.
Primeiro a gente isola nas duas equações:
Você pode usar uma identidade trigonométrica na segunda equação:
E o a gente já sabe, porque é a segunda equação. Mas dá pra usar aquela famosa relação e encontrar o seno também:
Substituindo isso e o na equação de antes:
Então:
E finalmente, elevando os dois lados ao quadrado:
Juntando esses termos que dependem de e usando :
Ok! Agora vamos interpretar essa equação.
Passo 2
Quando a gente tem uma elipse certinha, com os semieixos alinhados com e , a equação dela tem essa forma geral aqui:
No nosso caso, a gente tem uma situação mais parecidas com isso aqui:
Aquele termo ali no meio, que a gente chama de termo quadrático misto é um aviso: ele diz que a nossa elipse foi rotacionada por algum ângulo!
O nosso problema aqui é: que ângulo é esse?
Passo 3
Então tá, vamos supor que a nossa elipse é “certinha” no plano , , como na figura do enunciado.
A nossa equação é:
Se a gente rotacionar essa equação, pra escrever nas coordenadas e , aquele termo quadrático misto deve sumir!
Aqui é hora de lembrar de um resultado importante lá da geometria analítica. Quando você tem uma equação desse tipo aqui:
E quer aplicar uma rotação por um ângulo pra encontrar uma equação nessa forma aqui:
Existe uma fórmula pra saber qual é o ângulo que faz esse termo misto sumir! É essa aqui:
E olhando para a nossa equação, os coeficientes são:
Substituindo isso na fórmula de cima:
Beleza, agora vamos simplificar um pouco.
Passo 4
Primeiro resolvemos essa soma de frações no numerador:
Mas essa é a cotangente do ângulo. Invertendo os dois lados, vamos ficar com o tangente:
Agora dividindo em cima e embaixo por :
E levando aquele sinal negativo para o denominador:
Agora aquele termo ali em colchetes parece muito com uma identidade trigonométrica importante!
Ou seja, se , a gente pode reescrever aquela equação de cima como:
Pronto! Provamos a fórmula do enunciado! Esse é o ângulo de rotação entre os sistemas, que o enunciado chamou de :
Agora sim!
Resposta
Demonstração.