Exercícios de Polarização da Luz - Lista de Exercícios Resolvida

A componente magnética de uma onda luminosa polarizada é dada por

Determine:

1. A direção de polarização da luz.
2. A frequência da luz.

Obtenha a polarização da onda eletromagnética representada abaixo. Demonstre o tipo de polarização (linear, circular ou elíptica) e mostre, caso não seja linear, se a polarização é à esquerda ou à direita. Use a técnica vetorial usada em aula:

onde .

A componente magnética de uma onda polarizada é dada por . Determine:

1. A direção de propagação da onda.
2. A direção de polarização da luz.
3. Escreva uma expressão para o campo elétrico da onda, incluindo o valor do número de onda.
4. Determine o comprimento de onda.
5. Em que região do espectro eletromagnético está essa onda?

Em certa região do espaço, o campo magnético de um feixe luminoso é dado por

em unidades do SI.

Encontre a frequência angular e o comprimento de onda associados.

Ache o vetor campo elétrico por aplicação da Lei de Àmpere. Confira sua resposta

usando  .

Diga qual é o estado de polarização da luz, justificando.

Esse feixe luminoso incide perpendicularmente sobre um aparato de fenda dupla, tal que as fendas têm abertura desprezível e estão separadas de . A fenda superior (ver

figura) está coberta por uma fina lâmina cujo índice de refração é e tem espessura de .

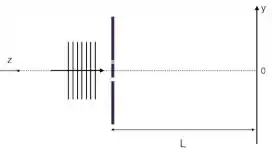
Logo após a saída das fendas, qual é a diferença de fase entre raios paralelos emergindo das fendas superior e inferior?

Em uma tela posicionada a do aparato, em que posição estará o máximo (deslocado) de ordem zero?

O campo elétrico de uma onda eletromagnética plana e monocromática que se propaga no vácuo é descrito por

onde , e são constantes positivas. Em função dos dados do enunciado e de constantes fundamentais, calcule o que se pede, justificando os cálculos.

a) Determine o comprimento de onda, o período de oscilação e a direção e o sentido de propagação dessa onda.

b) Determine a polarização da onda.

c) Determine o vetor campo magnético (módulo, direção e sentido) dessa onda eletromagnética.

Uma onda eletromagnética monocromática, viajando no sentido no vácuo, tem polarização circular direita e comprimento de onda igual a . Na origem e em o campo elétrico tem amplitude máxima dada por .

a) Escreve a expressão para o campo elétrico dessa onda, em função do tempo e espaço.

b) Encontre o campo magnético através da Lei de Faraday. Verifique a sua resposta através de .

c) Descreva duas maneiras de transformar o estado de polarização dessa onda para polarização linear.

– Obtenha a polarização da onda eletromagnética representada abaixo.

Demonstre o tipo de polarização (linear, circular ou elíptica) e mostre, caso não seja linear, se a polarização é à esquerda ou à direita através da técnica usada em aula:

; , onde .

– Obtenha a polarização da onda eletromagnética representada abaixo. Demonstre o tipo de polarização (linear, circular ou elíptica) e demonstre, caso não seja linear, se a polarização é à esquerda ou à direita.

Caso seja linear obtenha o ângulo de inclinação da reta entre os componentes e e faça um desenho dessa polarização no eixo :

; , onde .

Uma onda plana luminosa, polarizada ao longo do eixo se propaga na direção positiva do eixo (no vácuo).

Uma expressão possível para o campo elétrico da luz é:

Nenhuma das anteriores

Uma onda plana senoidal possui os seguintes campos elétrico e magnético, respectivamente, e .

A direção de polarização e o sentido de propagação dessa onda são dados, respectivamente, pelos vetores unitários:

1. e
2. e
3. e
4. e
5. A onda não é polarizada linearmente.

Obtenha a polarização da onda eletromagnética representada abaixo. Demonstre o

tipo de polarização (linear, circular ou elíptica) e mostre, caso não seja linear, se a

polarização é à esquerda ou à direita. Se for linear obtenha o ângulo θ de polarização.

Considere agora que esse feixe tem seu campo elétrico representado pela expressão

onde os eixos cartesianos estão orientados como mostrado na figura. Observa-se que, para determinado ângulo de incidência, o feixe de luz após reflexão (feixe emergente em 2) está linearmente polarizado.

(b) Qual é o estado de polarização do feixe incidente? Justifique.

(c) Qual é a direção de polarização do feixe refletido? Justifique.

(d) Qual é o ângulo de incidência para o qual esse efeito ocorre?

Responda corretamente e justifique suas opções:

c-( ) Duas ondas Eletromagnéticas coerentes e com polarizações perpendiculares entre si geram interferência ao se superporem.

Uma onda plana luminosa no vácuo, totalmente polarizada ao longo do eixo , se propaga na direção negativa do eixo . Uma possível expressão para o campo elétrico da luz é...?

O campo elétrico de uma onda plana eletromagnética monocromática no vácuo é dado por

1. Obtenha a expressão para o campo magnético associado a essa onda.
2. Discuta a evolução no tempo do campo elétrico na posição , por meio de um esboço de no plano de polarização. Que tipo de polarização esta onda apresenta?
3. Determine a média temporal do vetor de Poynting .
4. Considere uma bactéria de estrutura esférica de raio e massa que absorve completamente a radiação eletromagnética que a atinge (e não reflete), de baixo para cima.

Desprezando outros possíveis efeitos, determine o valor mínimo de para que a bactéria não caia sob o efeito da gravidade, se a onda plana aqui discutida for usada para suspendê-la (suponha que a superfície de absorção da bactéria seja um disco de raio ).

A polarização de uma onda eletromagnética está representada por

;

,

onde .

Demonstre o tipo de polarização (linear, circular ou elíptica) dessa onda. Caso seja linear não precisa determinar o ângulo de inclinação do vetor elétrico. Se for elíptica ou circular, não precisa demonstrar se a polarização é à esquerda ou à direita.

– Obtenha a polarização da onda eletromagnética representada abaixo.

Obtenha a equação que relaciona com a qual indique o tipo de polarização (linear, circular ou elíptica). Se a polarização não for linear, demonstre se ela é à esquerda (anti-horária) ou à direita (horária).

Caso seja linear, obtenha o ângulo de inclinação da reta entre os componentes e e faça um desenho dessa polarização no eixo .

; , onde .

A polarização de uma onda eletromagnética está representada por

;

,

onde .

(b) Demonstre o tipo de polarização (linear, circular ou elíptica) dessa onda. Caso não seja linear, não precisa demonstrar se a polarização é à esquerda ou à direita.

– Obtenha a polarização da onda eletromagnética representada abaixo. Demonstre o tipo de polarização (linear, circular ou elíptica) e mostre, caso não seja linear, se a polarização é à esquerda ou à direita através da técnica usada em aula:

; , onde .

Obtenha a polarização da onda eletromagnética representada abaixo. Demonstre o tipo de polarização (linear, circular ou elíptica) e mostre, caso não seja linear, se a polarização é à esquerda ou à direita. Use a técnica vetorial usada em aula:

, onde .

Um feixe de luz não polarizado atravessa dois polarizadores em sequência, cujos eixos de polarização estão orientados com e em relação à vertical, respectivamente, nessa ordem. Um terceiro polarizador é introduzido entre os dois anteriores com eixo de polarização em , em relação à vertical. Se a intensidade do feixo após passar pelos três polarizadores é nula, pode-se concluir

a) ou

b) somente.

c) somente.

d) ou .

Um feixe de luz de frequência natural de ilumina um filme fino de largura , conforme a figura abaixo, na qual e .

Considere uma incidência normal.

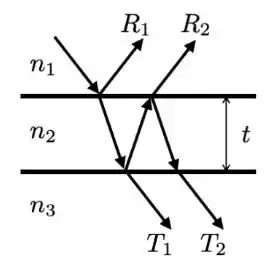
Determine, em função dos dados do enunciado e substituindo todas as constantes pelos seus respectivos valores,

i) os comprimentos de onda da onda nos meios e ;

ii) a diferença de fase entre os raios e (indique claramente como cada raio ganha determinada fase e sua diferença); e

iii) o menor valor de (com ) para que os raios e se interfiram construtivamente.

No experimento da dupla fenda de Young com fendas de larguras desprezíveis, observa-se que o centro de uma franja escura está localizada na posição da tela, em relação ao centro da imagem. Nesse experimento, a distância entre o plano da tela e o plano do anteparo é e a luz utilizada possui comprimento de onda de . Com esses dados, pode-se dizer que a distância entre as duas fendas é maior ou igual à (considere válida a aproximação de pequenos ângulos)

a)

b)

c)

d)

Em relação a um referencial inercial , no instante de tempo , uma partícula se encontra na posição , , ) e velocidade . Outra partícula possui velocidade e posição , , ), onde , em relação à . Um referencial inercial se move com velocidade de em relação ao referencial inercial . Determine, em função dos dados do enunciado e substituindo todas as constantes pelos seus respectivos valores, i) a posição e o instante de tempo, em relação ao referencial , para os quais a partícula alcança a partícula ; e ii) a velocidade relativa da partícula em relação ao referencial da partícula (módulo, direção e sentido).