Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 12.1 - Ex. 58
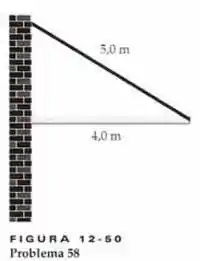
Um determinado tipo de viga de aço de construção pesa 22 libras por pé. Uma nova empresa chega à cidade e o contrata para pendurar sua placa em uma viga deste tipo, de 4,0 m de comprimento. O Projeto prevê que a viga se estende para fora da fachada de tijolos horizontalmente (Figura 12-50). Ela deve ser suportada por um cabo de aço de 5,0 m de comprimento. O cabo é preso a uma extremidade da viga e na fachada, acima do ponto em que a viga está em contato com a parede. Durante um estágio inicial da montagem, a viga não deve ser pregada na parede, mas deve mantida em posição apenas pelo atrito.
- Qual é o menor coeficiente de atrito, entre a viga e a parede, para que a viga permaneça em equilíbrio estático?
- Qual é, neste caso, a tração no cabo?
Passo 1
Então galera, o que está acontecendo aqui? Nós temos uma barra que deve ser mantida fixa pela parede e pelo cabo.
Dizemos então que a barra deve permanecer em equilíbrio estático. Mas o que isso quer dizer? O corpo está em equilíbrio quando duas condições são satisfeitas:
Agora vamos desenhar esta situação, colocando as forças que atuam sobre esta placa:
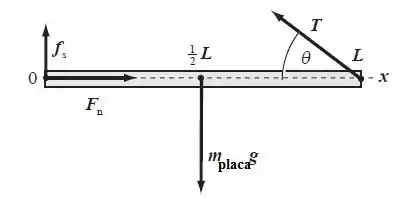
No centro de gravidade, ou seja, no ponto central da nossa placa, temos a força gravitacional sendo aplicada para baixo. Dada por:
Como nós temos duas superfícies em contato, existe a força normal perpendicular à superfície, que neste caso é a nossa parede. E a força de atrito , contrária ao movimento relativo entre a barra e a parede. E podem se relacionar como:
Como temos um cabo suportando a viga, temos uma força de tração (T), puxando nossa viga para cima e formando com a placa um ângulo . Como vamos precisar das forças nas direções x e y devemos desmembrar esta força de tração.
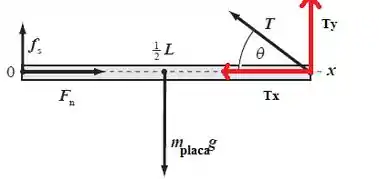
Sendo assim,
Agora ficou fácil ! Só precisamos fazer o somatório das forças e achar o coeficiente de atrito e a tração.
Passo 2
Vamos começar usando a primeira condição. Se , então .
Muito bem, agora vamos separar as forças. Na direção x nós temos a força normal e a tração, com sentidos opostos:
Substituindo
Na direção y, temos a força da gravidade, para baixo, e a força de atrito e a tensão, voltadas para cima:
Substituindo:
Lembrando que a massa da placa pode ser calculada pela multiplicação do seu comprimento (L) e sua densidade linear ():
Isolando o coeficiente de atito:
Substituindo
Calma que ainda não acabou ! Agora que achamos o coeficiente de atrito vamos para a tração.
Passo 3
Para achar a equação da tração vamos usar a segunda condição, . O torque é calculado como:
Onde r é a distância entre a força e o eixo de rotação. A escolha do eixo será muito importante, e aqui vamos escolher a lateral esquerda da barra, em contato com a parede, como nosso eixo.
Beleza ! Quando fazemos isso a força de atrito estará na posição . A força da gravidade terá enquanto a tração terá
Já temos r agora só precisamos saber o sentido de rotação. Por convenção se uma determinada força for capaz de girar o corpo no sentido anti-horário seu sinal será positivo. A força de tração é capaz de girar a barra no sentido anti-horário (+), já a força peso gira no sentido horário (-).
Jogando toda informação na segunda condição:
Substituindo as forças:
Isolando T:
Substituindo T na equação do coeficiente de atrito:
A figura formada pelos três componentes é um triângulo retângulo, cuja hipotenusa vale 5 m e o cateto adjacente, 4 m.
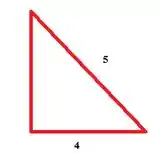
O cálculo do cateto oposto pode ser feito por:
Então:
Passo 4
Estamos quase lá! Já temos o coeficiente de atrito, agora falta calcularmos a tração. Nós já sabemos sua fórmula:
Também já temos todos os dados:
Como temos todas as unidades em metros devemos manipular
Substituindo: